Прямокутний трикутник
До речі, чи добре ти пам'ятаєш, що таке катети і гіпотенуза? Якщо не дуже, то дивись на малюнок - освіжай знання
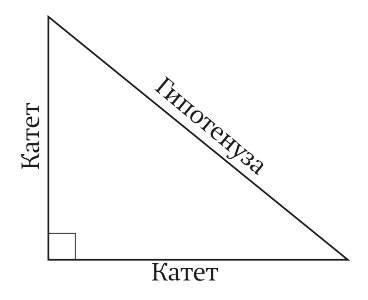
Цілком можливо, що ти вже багато разів використовував теорему Піфагора, а ось чи замислювався ти, чому ж вірна така теорема. Як би її довести? А давай зробимо, як стародавні греки. Намалюємо квадрат зі стороною $ latex a + b $.
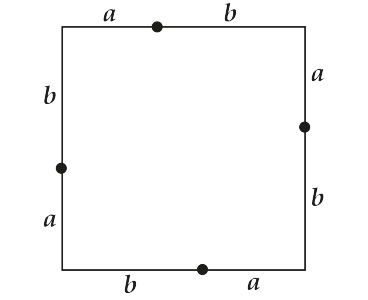
Бачиш, як хитро ми поділили його боку на відрізки довжин $ latex a $ і $ latex b $!
А тепер з'єднаємо відмічені точки
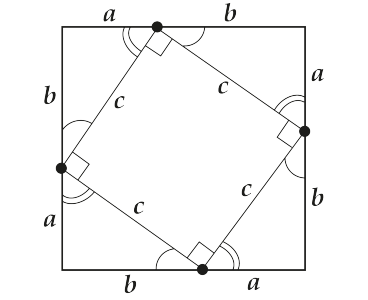
Чому ж дорівнює площа більшого квадрата? Правильно, $ latex ^> $. А площа меншого? Звичайно, $ latex c ^ 2 $. Залишилася сумарна площа чотирьох куточків. Уяви, що ми взяли їх по два і притулили один до одного гіпотенузи. Що вийшло? Два прямокутники. Значить, площа «обрізків» дорівнює $ latex \ displaystyle 2ab $.
Давай тепер зберемо все разом.
Ось і побували ми Пифагором - довели його теорему древнім способом.
Прямокутний трикутник і тригонометрія
Для прямокутного трикутника виконуються наступні співвідношення:

I. $ latex \ displaystyle \ sin \ angle A = \ frac; \ \ \ sin \ angle B = \ frac \ $
Синус гострого кута дорівнює відношенню протилежного катета до гіпотенузи
II. $ Latex \ displaystyle \ cos \ angle A = \ frac; \ \ \ cos \ angle B = \ frac $
Косинус гострого кута дорівнює відношенню прилеглого катета до гіпотенузи.
III. $ Latex \ displaystyle tg
\ Angle A = \ frac; \ \ tg
Тангенс гострого кута дорівнює відношенню протилежного катета до прилеглого катета.
IV. $ Latex \ displaystyle ctg
\ Angle A = \ frac; \ \ ctg
Котангенс гострого кута дорівнює відношенню прилеглого катета до протилежного катета.
І ще раз все це у вигляді таблички:

$ Latex \ displaystyle \ sin \ angle A = \ frac $
$ Latex \ displaystyle \ sin \ angle B = \ frac $
Прямокутні трикутники рівні, якщо катет і гострий кут одного трикутника відповідно рівні катета і гострому куту другого трикутника.
Увага! Тут дуже важливо, щоб катети були «відповідні». Наприклад, якщо буде так:
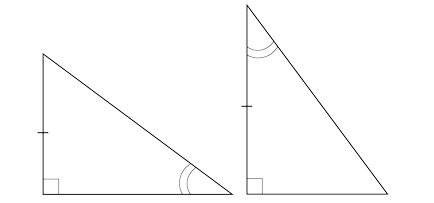
Те ТРИКУТНИКИ НЕ РІВНІ. незважаючи на те, що мають по одному однаковому гострого кута.
Потрібно, щоб в обох трикутниках катет був прилеглим, або в обох - протилежними.
Ти помітив, чим відрізняються ознаки рівності прямокутних трикутників від звичайних ознак рівності трикутників? Зазирни в тему «Трикутник» і зверни увагу на те, що для рівності «рядових» трикутників потрібно рівність трьох їх елементів: дві сторони і кут між ними, два кута і сторона між ними або три сторони. А ось для рівності прямокутних трикутників досить усього двох відповідних елементів. Здорово, правда?
Приблизно така ж ситуація і з ознаками подібності прямокутних трикутників.
Ознаки подібності прямокутних трикутників
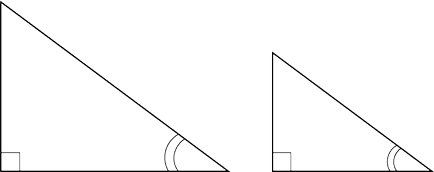
Якщо прямокутні трикутники мають по однаковому гострого кута. то вони подібні.