Пряма і площина геометрії Евкліда

Кілька тисячоліть математики намагаються, з одного боку, довести п'ятий постулат Евкліда, а з іншого боку, дивуються, навіщо він був доданий Евклидом до перших чотирьох.

П'ятий постулат завжди вважався зайвим.

Одна з його формулювань свідчить, - «На площині через точку, що знаходиться поза прямою, можна провести тільки одну пряму, паралельну даній».

Згадаймо прийняті Евклідом визначення і властивості:

З визначення «Точка є те, що не має частин» слід, що точка є відрізком прямої, довжина якого дорівнює його ширині. Отже, точка є частиною прямої або окремим випадком відображення прямий і, в той же час, довжина її і ширина не рівні нулю, так як в цьому випадку точка не існувала б;

З визначення «Пряма є така лінія, яка однаково розташована на всі точки» з попереднього визначення випливає, що пряма лінія - це площина, ширина якої дорівнює ширині точки.

Отже, пряма лінія - частина площини або окремий випадок відображення площині;

З визначення «Площина є поверхню, яка однаково розташована до всіх прямим на ній лежить» слід, що площину може складатися з точок, прямих ліній або інших площин збігаються з даної.

Звідси випливає, що площина це основне поняття, а точка і пряма є окремий випадок площині.

Продовжуючи міркувати в тому ж дусі, отримуємо крамольну думку, якщо основне поняття складається з окремих випадків, то і саме поняття має представляти окремий випадок.

У планіметрії Лобачевского-Бойяи через точку поза прямою на площині можна провести скільки завгодно різних прямих, паралельних даній. Це - аксіома.

У планіметрії Рімана через точку поза прямою можна провести жодної прямої, паралельної даній. І це твердження теж аксіоматізіруется. Здавалося б, що крамольного може бути в цих аксіомах? Де може бути неточність, яка стільки років ставить в тупик багатьох вчених? Неточність криється в одному визначенні і це визначення - поняття «ПЛОЩИНУ».

Постулювавши це визначення, як АБСОЛЮТНА ПЛОЩИНУ, ми потрапляємо в нереальний двовимірний світ барона Мюнхгаузена.

У реальному тривимірному світі - Площина є поверхню з радіусом кривизни, що прагнуть до нескінченності.

Звідси отримуємо, що Пряма є така лінія, яка однаково розташована на всі точки поверхні, з даними радіусом кривизни.

Радіус кривизни площини, а з нею і лінії може бути будь-яким і визначається він конкретними силами, що діють на площину в розглянутій кривої області, а не в прямокутної.

Звідси і реальна точка, що має довжину, ширину і товщину так само є кривою поверхнею. Для спростування цього спробуйте знайти пряму ділянку на поверхні кола або кулі.

Ймовірно, це і є те, що ставив під сумнів у своїй геометрії Евклід, вводячи в геометрію п'ятий постулат. П'ятий постулат надає площині Евкліда властивості АБСОЛЮТНО ПЛОСКОЇ поверхні. Введення поняття кривизни, виводить геометрію Евкліда з нереального плоского двовимірного світу в реальний кривої тривимірний світ.

Двовимірна абсолютно плоска геометрія Евкліда стає окремим випадком за умови, що радіус кривизни даної площині або кривої прагнути до нескінченності.

За часів Евкліда, ймовірно, не було поняття про кривизну простору, і навіть сама Земля розглядалася як абсолютно пласка поверхня.

Однак, Евклід, ймовірно, не погоджувався з таким визначенням.

Заява в ті часи, що Земля це крива поверхню, або тим більше куля, не було б правильно сприйнято.

Ймовірно, своїм п'ятим постулатом Евклід відправив «зашифроване повідомлення» до майбутнього людству, показуючи, що в його геометрії з площиною не всі йде нормально, що вона вигадана - гіпотетична, як його п'ятий постулат.

Постулювавши абсолютну площину, Евклід дав людству можливість створити зручні і прості для застосування: геометрію, математику, фізику і тим самим закласти фундамент для ривка в нескінченні простори кривого простору.

Визнання факту, про неможливість існування абсолютної площині, ось, мабуть, наріжний камінь в підставі створення нової геометрії, фізики, математики та шлях пізнання всесвіту.

Однак в науці досі прямокутний трикутник Піфагора, побудований на абсолютній площині геометрії Евкліда, є основою, у всесвітньо визнаних теоріях опису будови всесвіту.

Візьмемо перетворення Лоренца, в них значення √ 1 v 2 / c 2 отримано з прямокутника Піфагора.

Це суперечить букві і духу теорії кривизни простору. в якому немає місця плоскому прямокутному трикутнику, абсолютно прямій лінії і абсолютно плоскій поверхні.

Знову згадаємо Евкліда і його визначення точки.

«Точка є те, що не має частин». У реальному світі точка є геометричним тілом.

У постулатах Евкліда нічого не говориться про товщину точки.

У реальному світі точку можна уявити найменшим колом з відсутньою товщиною.

Якщо ми додамо до визначення точки ще й її товщину, то вона повинна являти собою найменший куля.

В такому випадку ми вже не можемо скористатися плоским трикутником Піфагора не мають товщину.

На точці-кулі, як би ми не зменшували його розмір, прямокутний трикутник матиме три прямих кута і цей трикутник ніяк не зможе стати плоским.

Нехтування значенням другого порядку малості при заміні трикутника на криволінійній поверхні прямокутним, плоским трикутником, в мікросвіті веде до величезної помилку.

Проводячи розрахунки для поверхонь, траєкторій руху, у яких радіус кривизни прагнути до нуля, отримуємо, що при прагненні до нуля площі трикутника Евкліда і Лобачевського, величина значення, другого порядку малості, тобто різниця площ або довжин в цих геометрії, набуває значення, трохи чи не рівне самої площі трикутників або відстаней між точками.

Легко уявити цю різницю, досить побудувати спрощену модель (рис.1) двомірного трикутника Евкліда в тривимірному трикутнику Лобачевського.

Площа трикутника Лобачевського S АВС = 4 πR 2/8 = πR 2/2

Площа трикутника Евкліда, розрахована на основі прямокутника Піфагора S АВС = R2√3 / 2

Як би R не прагнув до нуля, різниця площ плоского трикутника і трикутника на кулі буде відмінна приблизно на:

Нехтувати цією різницею або вважати цю неточність величиною другого порядку малості, яку можна не брати до уваги, явно не коректно.

Теж відбувається і з траєкторією руху точки А з нескінченності в нуль - точку В, коли радіус кривизни прагнути до нуля (рис.2).

На ділянці, де R → ∞ (рис.2 зліва) катет АВ, якщо застосувати прямокутний трикутник Піфагора практично дорівнює гіпотенузі і ми потрапляємо в фізику Ньютона

На ділянці АВ, де R → 0 (рис.2 праворуч), катет АВ перетворюється в хорду L. довжина якої обчислюється за формулою:

L 2 = a (2 R - a).

Висновок цієї формули наведено ще вIIIвеке в китайській книзі «Математика в дев'яти книгах» і в завданні індійського математікаVIIвека Брамагупти.

Опис траєкторії електрона і його спина на основі реальних тривимірних кривих і об'ємних трикутників. а не на основі ламаних двовимірних прямих і плоских прямокутників дозволить математикам потрапити всередину атома і розкрити таємниці невловимого простору.

Визнаючи неоціненний внесок фізиків, що працювали до третього тисячоліття, слід визнати, що вони не змогли розшифрувати таємницю послання Евкліда, закладену ним у п'ятий постулат.

Моделі матерії і простору, створені на основі прямокутного прямокутника Піфагора, слід визнати двомірними.

Третє тисячоліття має стати тисячоліттям створення основи, яка описує реальні тривимірні моделі криволінійної матерії і простору.

П'ятий постулат Евкліда в 3 D просторі.

Уявімо п'ятий постулат Евкліда в загальному вигляді в тривимірному просторі.

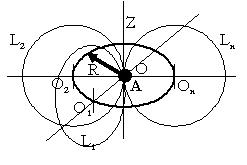
Через точку А (рис.3), заданої площині О1. має радіус кривизни прагне до нескінченності, з центром О1. проведемо пряму L 1, з радіусом кривизни прагнуть до нескінченності, і збігається з центром кривизни площини О1.

Перемістимо центр кривизни в точку О2. і проведемо через точку A пряму L 2. належить площині О2. з центром кривизни площини О2.

Як бачимо прямі L 1. L 2. не перетинаються, хоча мають спільну точку А.

Таким чином можна провести безліч паралельних прямих L 1. L 2. ..., L n → ∞ котрі належать до даної площини, але мають спільну точку А, за умови, що координати центру кривизни кожної площині О1. О2. ..., Про n → ∞, описують окружність Про радіусом кривизни R → ∞ навколо осі Z.

Вісь Z є спільною дотичною для всіх розглянутих площин.

В даному випадку ми отримуємо просторову фігуру тора, за однакової кількості R. У загальному випадку R може мати відмінні значення.

У реальному, фізичному просторі, радіус кривизни не нескінченний, а обмежений силами, які визначаються фізичними властивостями середовища і взаємодією даної області середовища з іншими областями. Ці властивості викликають деформацію радіуса кривизни площини як з будь-якої, так і по всьому її осях симетрії.

З п'ятого постулату слідують умови:

1. Координати Z площині, а значить і прямий і задається точки, як належать площині, рівні.

2. Одна з координат X або Y задається точки, не належить прямій.

3. Пряма має тільки одну ступінь свободи.

4. Центр кривизни прямий, паралельної заданій, для дотримання паралельності може переміщатися тільки по одній осі.

Звідси, п'ятий постулат Евкліда, є окремий випадок, що описує, єдиний варіант з незліченної безлічі.

На площині, із заданим радіусом кривизни, через точку, що знаходиться поза прямою. можна провести тільки одну пряму, паралельну даній, у якій хоча б одна з координат центру кривизни не співпадала з координатою центру кривизни вихідної.

Таке тлумачення п'ятого постулату в загальному вигляді описує просторову трубу (рис.4) з радіусом кривизни R → ∞.

Введення поняття кривизни в опис площині і прямих, веде до парадоксального висновку:

Будь-яка пряма при її нескінченному продовженні є замкнутою кривою.

Дійсно, якщо у прямій є радіус кривизни, значить, є і окружність, яку вона формує, незалежно якого радіусу, аж до нескінченного.

Звідси у кривої прямий немає початку і немає кінця.

Крива, виникаючи з нескінченності виконавши свій шлях і, крутанувшісь по нескінченному простору, знову йде в нескінченність.

Як можна відрізнити одну пряму від іншої?

Якщо брати координати початку і кінця прямої, то вони знаходяться в невизначеній нескінченності.

А якщо порівнювати радіуси кривизни «прямих»?

В цьому випадку ми відразу зможемо відрізнити одну пряму від іншої.

У реальному фізичному світі все звичайно. Значить і радіуси кривизни «прямих» і «площин» кінцеві.

Чи означає це про кінцівки нашого всесвіту?

Адже згідно побудованої моделі кривої геометрії виходить, що якщо подолати площину з радіусом кривизни, що прагнуть до нескінченності можна потрапити в потойбічний світ. Однак на цьому шляху нас зустріне НЕПЕРЕБОРНА АБСОЛЮТНО ПРЯМА дотичних до кривої.

А абсолютно пряма лінія в реальному природі не існує (див. Нижче).

В принципі, «намалювати» таку геометрію можна.
Для цього достатньо скористатися геометрією Рімана.
Однак тут виникає питання.
Чи можливо рух в такій геометрії?
У цьому випадку ми повинні визнати, що існує відцентрове прискорення, тобто рух з прискоренням має негативний радіус-вектор кривизни.
Реальне фізичний рух відбувається при додатку імпульсу сили (І.С.) за величиною перевершує величину сил реакції хвильового поля чинного на тіло в стані инерциального спокою.
Виникає питання.
По якій траєкторії, відбувається рух під дією І.С.
За відцентрової або центростремительной?
Питання це актуальне тим, що відповідь на нього визначає яку геометрію треба застосовувати для опису траєкторії руху.
Якщо це доцентровий рух, то траєкторія руху повинна описуватися реальними кривими геометрії Лобачевського. Тобто центр кривизни лежить всередині вписаного кола.
Якщо це відцентровий рух, то траєкторія руху повинна описуватися уявними кривими геометрії Рімана. Тобто центр кривизни лежить поза вписаного кола.

Для прикладу розглянемо рух ракети під час розгону.

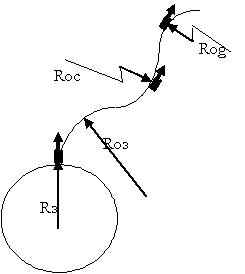
Під час старту на стартовому столі радіус кривизни траєкторії руху ракети дорівнює радіусу Землі R З (рис.5).
Як відомо, при розгоні ракети вона залишається на орбіті навколо Землі, якщо не буде перевищена перша космічна швидкість.
Це, в свою чергу, означає переважання доцентрових сил від дії сил гравітаційного поля, утвореного Земним кулею.
Траєкторія руху ракети при цьому є доцентровою з радіусом кривизни R оз спрямованим в бік Землі. При досягненні другої космічної швидкості ракета виходить за межі дії гравітаційного поля Землі.
Чи означає це, що траєкторія ракети стала відцентрової?
Відповідь очевидна - ні.
В цьому випадку траєкторію руху ракети визначає гравітаційне поле Сонця. Траєкторія руху ракети при цьому залишилася центростремительной, але з радіусом кривизни R ос спрямованим в бік Сонця. Тобто змінилося тільки положення центру кривизни.
Той же результат ми отримуємо, розглядаючи третю космічну швидкість, при якій ракета летить по радіусу кривизни Rog. Центр цього радіусу визначає місце розташування центру галактики і т.д.
Таким чином, розглядаючи будь-який рух, ми не зможемо знайти природу і вид дії відцентрових сил.
Визнання існування відцентрових сил веде до визнання факту існування потойбічного світу і можливості руху по уявним траєкторіях, що суперечить існуванню реального світу.
Крім того, щоб перейти з геометрії Евкліда, з реальним радіусом R. в геометрію Рімана, з уявним радіусом - R. необхідно подолати абсолютно пряму дотичну, до кривизни якої прагнути пряма, при нескінченному радіусі кривизни R рис.6.

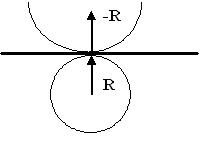
Для подолання дотичній, при переході руху з реальної геометрії Лобачевського в уявну геометрію Рімана рух, з криволінійного центростремительного, спочатку має перетворитися в АБСОЛЮТНО прямолінійний і тільки потім потрапити в потойбічний світ - криволинейного відцентрового руху.
Але абсолютно прямолінійний рух має на увазі АБСОЛЮТНЕ рівність сили дії силі протидії, що заперечує можливість будь-якого руху.
Це, ймовірно, є геометричне доказ відсутності відцентрового руху.
Але, як було зазначено раніше, рух по АБСОЛЮТНО прямий дотичній не існує. Тобто матерія, простір, в цьому випадку зникають, так як зникають будь-які сили.

F = Сила дії - Сила протидії = 0

Проте домінування в науковому світі думки про існування відцентрових сил призвело до того, що все осі координат, яке право застосовується математичному апараті мають напрямок від центру рис.7, тобто уявне напрямок, а не в центр, дійсне - реальний напрям рис.8.

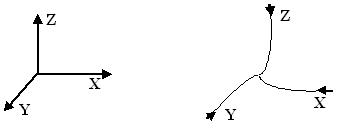
рис.7 Рис.8
Уявні, прямі, Криві, дійсні
осі координат осі координат

Це призводить до значних помилок при математичному описі, матерії, простору і реєстрованих природні явища.
У кривому просторі, при русі по криволінійних траєкторіях, самі осі координат також повинні бути криволінійними, рис.8.
Визначення.
Фізичне поступальний рух, це рух хвилі, середовища, тіла, матерії по центростремительной траєкторії з кривизною спрямованої в бік дії сил опору.
Центр радіусу кривизни фізичного поступального руху, знаходиться з внутрішньої сторони кривизни, розглянутого ділянки траєкторії руху.
Виходячи їх викладеного, можна припустити, що для здійснення заповітної мрії людства - польоту в безмежні космічні дали, ракеті необхідно вийти на траєкторію з радіусом кривизни, що прагнуть до нескінченності, тобто близької до абсолютної прямої з'єднує дві точки простору.