Презентація на тему теорема косинусів теорема (косинусів)
Презентація на тему: "Теорема косинусів Теорема (косинусів). Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін." - Транскрипт:
1 Теорема косинусів Теорема (косинусів). Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними, c 2 = a 2 + b 2 - 2ab cos C. Доказ: Позначимо АВ = с, ВС = а, АС = b. З вершини А опустимо перпендикуляр АD. Тоді АD = b sin C, CD = b cos C, BD = a - b cos C. За теоремою Піфагора маємо c 2 = (a - b cos C) 2 + (b sin C) 2 = a 2 - 2ab cos C + b 2 cos 2 C + b 2 sin 2 C = a 2 + b 2 - 2ab cos C. Самостійно розгляньте випадки прямого і тупого кута С.

2 Вправа 1 В трикутнику ABC AC = BC = 1, кут C дорівнює 30 о. Знайдіть AB. Відповідь.

3 Вправа 2 У трикутнику ABC AC = BC, кут C дорівнює 30 о, AB = 1. Знайдіть AC. Відповідь.

4 Вправа 3 У трикутнику ABC AC = BC = 1, кут C дорівнює 45 о. Знайдіть AB. Відповідь.

5 Вправа 4 У трикутнику ABC AC = BC, кут C дорівнює 45 о, AB = 1. Знайдіть AC. Відповідь.

6 Вправа 5 В трикутнику ABC AC = BC = 1, кут C дорівнює 150 о. Знайдіть AB. Відповідь.

7 Вправа 6 У трикутнику ABC AC = BC, кут C дорівнює 150 о, AB = 1. Знайдіть AC. Відповідь.

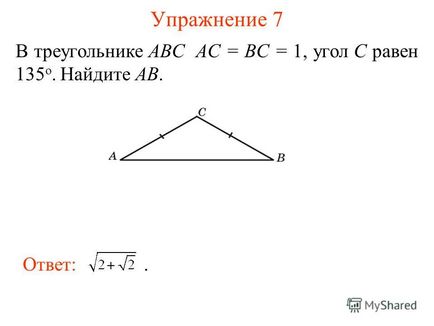
8 Вправа 7 У трикутнику ABC AC = BC = 1, кут C дорівнює 135 о. Знайдіть AB. Відповідь.
9 Вправа 8 У трикутнику ABC AC = BC, кут C дорівнює 135 о, AB = 1. Знайдіть AC. Відповідь.

10 Вправа 9 Дано три сторони трикутника a = 2, b = 3, c = 4. Знайдіть косинуси його кутів A, B, C. Відповідь: cos A =, cos B =, cos C =.

11 Вправа 10 Відповідь: В трикутнику АВС АВ = 12 см, АС = 8 см, кут A дорівнює 60 о. Знайдіть третю сторону.

12 Вправа 11 Відповідь: а) 14 см; Знайдіть сторону трикутника, що лежить проти кута в 120 о, якщо прилеглі до нього сторони рівні: а) 6 см і 10 см; б) 14 мм і 16 мм. б) 26 мм.

13 Вправа 12 Відповідь: а) гострий; При яких значеннях кута А квадрат сторони трикутника, що лежить проти цього кута: а) менше суми квадратів двох інших сторін; б) дорівнює сумі квадратів двох інших сторін; в) більше суми квадратів двох інших сторін? б) прямий; в) тупий.

14 Вправа 13 Відповідь: а) тупоугольного; Не вважаючи кути трикутника, вкажіть його вид (щодо кутів), якщо сторони трикутника рівні: а) 7, 8, 12; б) 0,3, 0,4, 0,5; в) 13, 14, 15. б) прямокутний; в) гострокутний.

15 Вправа 14 Відповідь: а) На стороні трикутника; Як розташований центр описаного кола щодо трикутника, сторони якого рівні: а) 6, 8, 10; б) 4, 5, 6; в) 3, 4, 6? б) всередині трикутника; в) поза трикутником.
16 Вправа 15 Дано діагоналі паралелограма з і d і кут між ними. Знайдіть сторони паралелограма. відповідь:
17 Вправа 16 Дано сторони паралелограма а й b і один з його кутів. Знайдіть діагоналі паралелограма. відповідь:
18 Вправа 17 Доведіть, що сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін. Доведення. По теоремі косинусів маємо Складаючи ці рівності і враховуючи, що косинус кута ADC дорівнює мінус косинус кута BAD, отримаємо необхідну твердження.
19 Вправа 18 Сторони паралелограма дорівнюють 30 мм і 35 мм, одна діагональ 55 мм. Знайдіть іншу діагональ. Відповідь: 35 мм.
20 Нехай в трикутнику ABC AB = c, AC = b, BC = a. Доведіть, що для медіани m c, проведеної з вершини C, має місце формула Доказ. По теоремі косинусів, застосованої до трикутниках ACD і BCD, маємо: Складаючи ці рівності, отримаємо рівність з якого безпосередньо слід бажана формула. Вправа 19
21 Сторони трикутника дорівнюють 11, 12 і 13. Знайдіть медіану, проведену до більшої стороні. Вправа 20 Відповідь. 9,5.
22 У трикутник бічні сторони рівні 4. Знайдіть основу цього трикутника, якщо медіана, проведена до бічної сторони, дорівнює 3. Вправа 21 Відповідь.
23 Нехай в трикутнику ABC AC = b, BC = a. Доведіть, що для бісектриси l c, проведеної з вершини C, має місце формула де c, c - відрізки на які бісектриса ділить сторону AB Доказ. По теоремі косинусів, застосованої до трикутниках ACD і BCD, маємо: Помножимо першу рівність на a, друге на b і віднімемо з першого рівності друге. Роблячи тотожні перетворення, отримаємо рівність з якого безпосередньо слід бажана формула. Вправа 22
24 У трикутнику ABC AC = 3, BC = 4, AB = 5. Знайдіть бісектрису CD. Вправа 23 Відповідь:
25 У трикутнику ABC AC = BC = 20, AB = 5, Знайдіть бісектрису AD. Вправа 24 Відповідь: 6.
26 У трикутнику ABC AC = 12, BC = 15, AB = 18, Знайдіть бісектрису СD. Вправа 25 Відповідь: 10.
27 У трикутнику ABC AC = BC, AD - бісектриса, AB = CD = 1. Знайдіть AC. Вправа 26 Відповідь:
28 Вправа 27 Чи можна описати коло близько чотирикутника зі сторонами 1 см, 2 см, 3 см, 4 см? Більш точне формулювання: чи існує чотирикутник зі сторонами 1 см, 2 см, 3 см, 4 см, біля якого можна описати коло? Рішення. Близько чотирикутника ABCD можна описати коло в разі, якщо За теоремою косинусів Звідки Отже, такий чотирикутник існує.