поняття деконволюции
При досить складному фізичному поданні в тимчасовій (координатної) області деконволюції проста для розуміння в частотному поданні. Припустимо, що в будь-якої реєструючої системи відбувається резонансне поглинання енергії і зсув по фазі певного гармонійного коливання в складі вхідного сигналу, наприклад, перетворення гармоніки sin w0 t ® 0.5 sin (w0 -p / 4). Відповідно, для відновлення первісної форми сигналу операція деконволюции повинна виконати посилення даної гармоніки в вихідному сигналі в 2 рази і здійснити зворотний зсув фази на p / 4. Для однієї гармоніки виконання такої операції праці не представляє. Але практичні завдання деконволюции значно складніше, так як потрібно, як правило, відновлення повного спектру вихідного сигналу, що має безперервний характер.
Визначення деконволюции. Якщо для прямої згортки дискретного сигналу x (k) c імпульсним відгуком h (n) лінійної системи (фільтра) маємо рівняння:
y (k) = h (n) # 9314; x (k) ó H (z) X (z) = Y (z), Y (z) = yk z k. z = exp (-jj),
то завдання деконволюции в загальній формі - визначення сигналу на вході лінійної системи за значеннями вихідного сигналу, тобто зняття реакції (імпульсного відгуку) системи на сигнал і відновлення вихідної форми сигналу, що досить актуально, наприклад, для реєструючих систем:
X (z) = Y (z) / H (z) = Y (z) H-1 (z) ó y (k) # 9314; h -1 (n) = x (k), (13.1.1)
де індексом "-1" символічно позначена передавальна функція оператора зворотного фільтра H-1 (z) = 1 / H (z), тобто оператора деконволюции, інверсного прямому оператору згортки (імпульсного відгуку системи). Відповідно, при зворотному z-перетворення отримуємо оператор деконволюции:
H-1 (z) = 1 / H (z) ó h -1 (n). (13.1.2)
Очевидно, що якщо має місце H (z) H-1 (z) = 1, то при зворотному z-перетворення цього виразу ми повинні мати:
H (z) H-1 (z) = 1 ó h (n) # 9314; h -1 (n) = do (n), (13.1.3)
де do (n) - імпульс Кронекера. При цьому послідовна згортка сигналу x (k) з оператором системи h (k) і оператором деконволюции h -1 (k) буде еквівалентна згортку сигналу x (k) з імпульсом Кронекера, що не повинно змінити форму сигналу x (t).
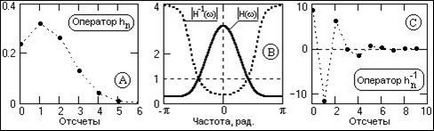
При z = exp (-jj) все викладене дійсно і для спектрального уявлення операторів. Приклад інверсії оператора через спектральне подання наведено на рис. 13.1.1 (вихідний оператор hn ® спектральна щільність H (# 969;) ® інверсна спектральна щільність H-1 (# 969;) ® інверсний оператор h -1 n на початковому інтервалі відліків).
Особливості деконволюции. Вираз (13.1.2) дозволяє зробити деякі висновки про особливості виконання деконволюции.
При обмеженою імпульсної реакції h (n) інверсний оператор h -1 (n) в загальному випадку не обмежений. Так, наприклад, якщо імпульсна реакція представлена нормованим диполем h (n) = ó (1 + az) = h (z), то маємо:
H-1 (z) = 1 / (1 + az) = 1-az + a 2 z 2 -a 3 z 3 +.
Це дійсно практично для будь-яких операторів згортки, енергія яких на будь-яких обмежених ділянках головного частотного діапазону близька до нульової. При інверсії спектральної функції таких операторів на цих ділянках виникають різкі спектральні піки, які при зворотному перетворенні Фур'є дають повільно затухаючі функції операторів. Приклад такого явища наведено на рис. 13.1.2.
Звідси випливає, що для точного виконання деконволюции необхідно розташовувати нескінченно довгим інверсним оператором фільтра. Практично, деконволюції виконується, якщо інверсний оператор досить швидко згасає і може бути обмежений. Але використання усічених операторів призводить до появи певної похибки деконволюции, величину якої слід контролювати.
Зауважимо також, що передавальні функції систем, як правило, мають низькочастотний характер. Інверсія операторів таких систем завжди пов'язана з посиленням високих частот, що призводить до високих коефіцієнтів посилення інверсними фільтрами дисперсії перешкод, що може призводити до втрати корисного сигналу серед посилених шумових флуктуацій.
Крім того, швидке загасання оператора деконволюции є необхідним, але ще не достатньою умовою реалізації деконволюции.
Стійкість фільтрів деконволюции. Функція H (z) в натуральному вираженні (13.1.2) має особливі точки - нулі функції, які стають полюсами функції H-1 (z) = 1 / H (z) і визначають стійкість інверсного фільтра. Для того щоб фільтр деконволюции був стійким, ряд 1 / H (z) має сходитися, тобто полюса функції повинні знаходитися поза одиничного кола на z-площині (всередині кола при використанні символіки z -1).
Многочлен H (z) порядку N може бути розкладений на N простих співмножників - Двочленні (диполів):
де а, b, с, ... - корені полінома. Звернення передавальної функції:
Якщо кожен з диполів функції (13.1.4) є мінімально-фазовим діракоідом, тобто коріння диполів знаходиться поза одиничного кола на z-площині і модулі нульових членів диполів завжди більше наступних за ними перших членів (в даному випадку: | а |> 1, | b |> 1, | з |> 1), то функція H ( z) також є мінімально-фазовим діракоідом. Максимум енергії імпульсного відгуку мінімально-фазового діракоіда зосереджений в його початковій частини і послідовність відліків є затухаючий ряд. При цьому функція 1 / H (z) також буде представляти собою передавальну функцію мінімально-фазового оператора, що забезпечує виконання умови (13.1.3), а її зворотне перетворення - сходиться ряд сталого фільтра. Так, наприклад, фільтр, який реалізує передавальну функцію (13.1.5), в самій загальній формі може бути виконаний у вигляді включених послідовно фільтрів, кожний з яких має передавальну функцію наступного типу (для першого фільтра):
Звідси, так само як і безпосередньо з виразу (13.1.5), слід також, що чим більше значення модулів коренів фільтра (далі від одиничного кола полюс фільтру), тим швидше затухає інверсний оператор.
Перевірка стійкості оператора інверсного фільтра в середовищі Mathcad приведена на рис. 13.1.3. Модулі всіх коренів більше 1, полюси інверсного полінома знаходяться за межами одиничному колі на z-площині, і інверсний оператор повинен бути стійкий.
На малюнку показаний також оператор деконволюции, який отриманий зворотним перетворенням Фур'є передавальної функції Hi (w). Оператор нескінченний, але загасає досить швидко, що забезпечує високу точність деконволюции при використанні обмеженого числа членів оператора фільтра (встановлюється користувачем по заданій точності).
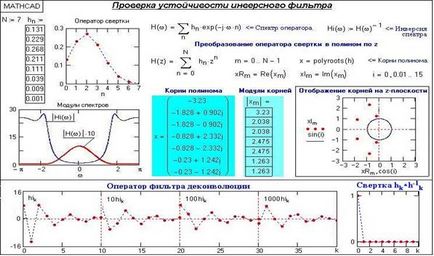
Мал. 13.1.3. Приклад сталого інверсного фільтра.
Приклад 2. Зрушимо вищенаведений оператор на одну позицію вправо і для збереження тієї ж енергії оператора приймемо h0 = 0.001. Потрібно оцінити стійкість інверсного оператора згортки hn =, N = 7.
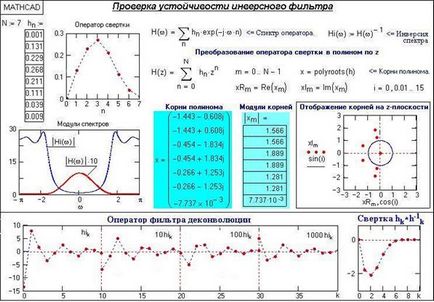
Мал. 13.1.4. Приклад нестійкої інверсного фільтра
Результати перевірки на стійкість нового оператора деконволюции наведені на рис. 13.1.4. При подібною формою операторів згортки модулі спектрів операторів практично не відрізняються. Але за рахунок зсуву по фазі даного оператора щодо першого (на рис. 13.1.3) коріння його z-полінома зазнали суттєва зміна, а модуль одного з коренів менше 1. І хоча обчислений оператор деконволюции також є ряд з кінцевої енергією, але умова (13.1.3) не виконується, про що наочно свідчить результат згортки hk * h -1 k.
Звернення недіракоідних функцій. Якщо H (z) - реверсоід, тобто коріння складових його диполів знаходяться всередині і на одиничному колі в z-площині, то стійке звернення H (z) є антіімпульсом (з негативними ступенями z) і для його використання необхідно мати у своєму розпорядженні "майбутніми" значеннями вхідного сигналу.
Якщо диполі функції (13.1.4) представляють собою і діракоіди, і реверсоіди, то звернення буде центроїдом і визначається повним рядом Лорана:
тобто оператор інверсного фільтра є двостороннім і не обов'язково симетричним, як ми зазвичай розглядали раніше двосторонні оператори.
Приклад 3. Передавальна функція фільтра: H (z) = 1-2z. Інверсна функція H-1 (z) = 1 / (1-2z). Частотні спектри функцій наведені на рис. 13.1.5.
Полюс функції zp = 1/2 і знаходиться всередині одиничного кола на z-площині.
Перепишемо вираз для інверсного фільтра в наступному вигляді:
Цей вислів є розкладанням в ряд за ступенями 1 / z і сходиться до кола радіусом 1/2 при z → ¥. Коефіцієнти при ступенях 1 / z є, відповідно, коефіцієнтами інверсного фільтра з координатами (-n), тобто фільтр оперує з "майбутніми" отсчетами вхідного сигналу (див. рис. 13.1.5).