Початкові геометричні поняття
Одна з найдавніших математичних наук - геометрія. Це вивчення фігур, їх властивостей і взаємного розташування.
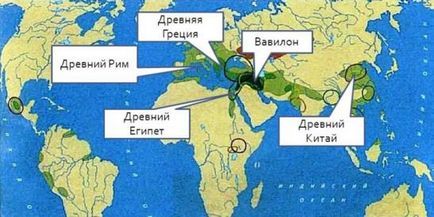
Перші геометричні факти знайдені в вавилонських клинописних таблицях і єгипетських папірусах (III тисячоліття до нашої ери), а також в інших джерелах. Сама назва науки давньогрецького походження. Назви багатьох фігур походить від грецького і латинського (древній Рим) мов.
Для створення фігур будемо використовувати точки і прямі. За допомогою цих фігур ми визначимо всі інші геометричні фігури, а точку і пряму спробуємо уявити: точку - як щось нескінченно маленьке, а пряму - як щось нескінченно тягнеться в обидві сторони.
Точки позначаються великими латинськими літерами, прямі позначаються однією маленькою латинською літерою або двома великими латинськими літерами. Словами описати взаємне розташування точок і прямої можна так:
- Точка знаходиться (лежить) на прямій або пряма проходить (проведена) через точку;
- Крапка не перебуває (не лежить) на прямій або пряма не проходить (не проведено) через точку.
Частина прямої, обмежену двома точками і точки, називають відрізком.
Частина прямої, обмежену однією точкою і точку, називають лучем.
Промені з загальною початковою точкою на одній прямій називають додатковими або протилежними.
Для назви відрізка послідовність літер не має значення, тобто, відрізок \ (AB \) той же відрізок \ (BA \).
Для назви променя важливо як першу букву писати початкову точку променя.
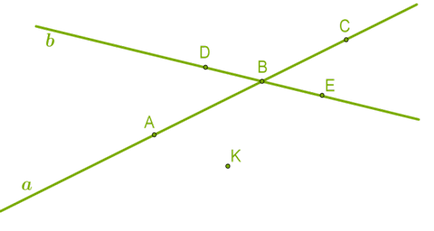
намальовані прямі \ (a \) і \ (b \), можна сказати також прямі \ (AC \) і \ (DE \);
дані прямі також проходять через точку \ (B \), вони перетинаються в цій точці;
точка \ (K \) не перебуває на одній прямій, тобто дані прямі не проходять через цю точку;
на прямий \ (a \) знаходяться відрізки \ (AC \), \ (AB \), \ (BC \), у відрізків \ (AB \) і \ (BC \) загальна кінцева точка \ (B \);
протилежні промені \ (BA \) і \ (BC \) знаходяться на прямій \ (a \), протилежні промені \ (BD \) і \ (BE \) знаходяться на прямій \ (b \).