Побудова кривої провисання і визначення стріл провисання - проектування механічної частини вл
Сторінка 4 з 37
Побудова кривої провисання проводу і визначення стріл провисання
Загальні відомості. Допустимі напруги в проводі
Жорсткість проводів і тросів позначається тільки при підвісці коротких відрізків проводів, наприклад, довжиною в кілька метрів між гірляндами анкерних опор. При довжині прольотів, прийнятих на повітряних лініях електропередачі, жорсткістю проводів можна знехтувати і розглядати їх як ідеальні гнучкі нитки, підвішені в двох точках і піддаються впливу рівномірно розподіленого навантаження від власної ваги дроти. Така гнучка нитка прийме обрис ланцюгової лінії, як показано на рис. 2.11 [3, 11, 13].
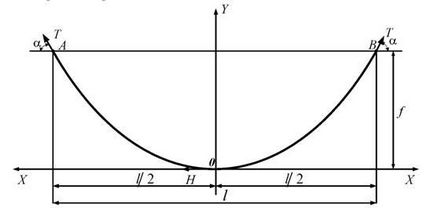
Мал. 2.11. Крива провисання проводу при однаковій висоті точок підвісу.
Згідно позначенням на рис. 2.11, відстань по горизонталі між точками підвісу А і В називається прольотом і позначається буквою l. Відстань по вертикалі в середині прольоту між проводами і прямий АВ, що з'єднує точки підвісу, називається стрілою провисання проводу і позначається буквою f. Обидві величини вимірюються в метрах. Сила, що діє в будь-якій точці дроти і спрямована по дотичній до кривої провисання, називається тяжіння і позначається буквою Т. тяжіння в нижчій точці кривої провисання, спрямоване горизонтально, прийнято позначати буквою Н. Обидва види тяжіння вимірюють в деканьютонах (даН) або кілограм - силах (кгс).
Сила, що діє на одиницю перетину дроту, називається напругою, позначається буквою # 963; і визначається за формулою:
(2.10)
даН / мм. кгс / мм,
де T - тяжіння в проводі, кгс (даН);
f - поперечний переріз проводу, мм.
Згідно [13], механічний розрахунок проводів і тросів проводиться за методом допустимих напружень, згідно з яким необхідною умовою є робота дроти в межах пружності його матеріалу, тобто напруги # 963 ;, що виникають в проводах або тросах при
впливі найбільшого навантаження або найнижчої температури, повинні бути менше межі міцності матеріалу провідника.
Допустиме максимальне напруження в проводі або тросі (даН / мм) визначається в залежності від тимчасового опору матеріалу дроти # 963; # 914; (ДаН / мм) і прийнятого коефіцієнта запасу міцності n за формулою:
(2.11)
В [13] допустимі напруження встановлені для трьох вихідних умов: 1) при найбільшому навантаженню; 2) при найнижчою температурі; 3) при середньорічній температурі. При цьому значення допустимих напружень при найбільшому навантаженню і найнижчою температурі мають однакові чисельні значення [13, стр. 324, 325, табл. 2.5.7].
Визначення стріли провисання проводу
Визначення стріли провисання проводу при довжині прольотів менше 800 метрів
Якщо довжина прольоту повітряної лінії електропередачі становить менше 800 м, розрахунок стріли провисання проводу виробляють за рівнянням параболи [3, 11].
Для виведення рівняння кривої провисання проводу приймемо систему координат з початком в нижчій точці кривої провисання О, віссю абсцис X і віссю ординат Y, як показано на рис. 2.12.
При виведенні використовуються основні рівняння статики для системи, що знаходиться в рівновазі:
а) сума проекцій всіх зовнішніх сил на координатні осі дорівнює нулю:
# 931; X = 0; # 931; y = 0; (2.12)
б) сума моментів всіх зовнішніх сил або їх проекцій щодо будь-якої точки дорівнює нулю:
# 931; м = 0. (2.13)
Розглянемо частину проводу, розрізавши його в нижчій точці О і в будь-якій точці D з координатами (х; у). Відрізані частини проводу замінимо відповідними тяжіння: в нижчій точці кривої провисання тяжіння Н, а в точці D тяжіння Т.
Так як для повітряних ліній дотична до кривої провисання в будь-якій точці має малий кут з горизонтальною прямою, то вага даної ділянки можна прийняти рівномірно розподіленим по горизонталі і замінити зосередженої силою рх, діючу пенсійну систему
середині розглянутого ділянки, тобто на відстані х / 2 від точок О і D, а силу тяжіння Тх прирівнюють до сили тяжіння в найнижчою точці Н.
Напрямок дії сили Н в точці D протилежно по відношенню до напрямку цієї ж сили в найнижчою точці кривої провисання проводу, так як внаслідок властивостей ідеальної гнучкої нитки вона може працювати тільки на розтягування.
У цьому випадку рівняння моментів сил відносно точки D запишеться наступним чином:
(2.14)
Вирішивши рівняння (2.14) щодо у, отримаємо основне рівняння кривої провисання проводу:
2
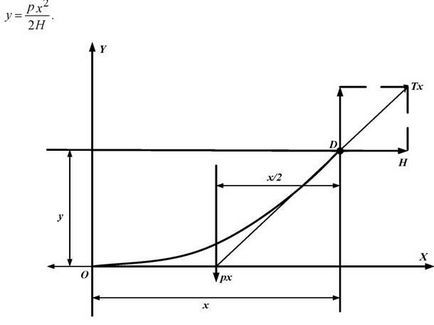
Мал. 2.12. Зовнішні сили, що діють на відрізок проводу
У формулу (2.15) входять: одинична навантаження на провід p і тяжіння в нижчій точці кривої провисання H. У практичних же розрахунках користуються не тяжіння, а напругою в проводі # 963 ;, і не одиничної навантаженням, а питомою # 947 ;. Підставляючи в формулу (2.15) p = # 947; F і H = gF. отримаємо:
(2.16)
Визначення стріли провисання проводу при однаковій висоті точок підвісу
Для визначення стріли провисання при однаковій висоті точок підвісу досить підставити в формулу (2.16) значення x = I / 2, тоді
(2.17)
Визначення стріли провисання проводу при різній висоті точок підвісу
При різній висоті точок підвісу крива провисання проводу буде несиметричною і нижча точка кривої провисання проводу буде знаходитися не в середині прольоту, а ближче або до точки А, як показано на рис. 2.13, або до точки В [3, 11].
В цьому випадку необхідно визначати три різні стріли провисання:
- fc - стріла провисання в середині прольоту, знаходиться за висловом, тотожному висловом для стріли провисання при однаковій висоті точок підвісу дроти, формула (2.17);
- fa - стріла провисання проводу, яка вимірюється щодо ординати нижчої точки підвісу А, знаходиться за формулою:
- fb - стріла провисання проводу, яка вимірюється щодо ординати вищої точки підвісу В, знаходиться за формулою:
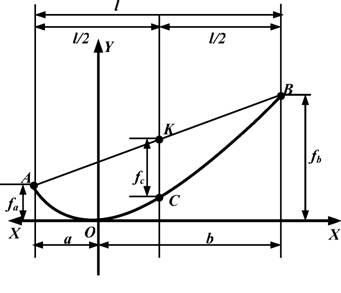
Мал. 2.13. Крива провисання проводу з різною висотою точок
підвісу
Визначення стріли провисання проводу при довжині прольотів більш ніж 800 метрів
При довжинах прольотів більш ніж 800 м похибка значення стріли провисання, яка визначається за формулою (2.16), перевищує допустиму. У цьому випадку користуються формулою, виведеною не з рівняння параболи, а з рівняння ланцюгової лінії, і визначають стрілу провисання по двучленной формулою:
(2.20)
Рішення про те, чи припустимо знехтувати другим членом формули (2.20) чи ні, робиться на підставі обчислень стріли провисання. Якщо числове значення другого члена формули (2.20) буде менше ніж 0,1% від значення стріли провисання, то тільки в цьому випадку їм можна знехтувати.
приклад 2.2
Користуючись результатами прикладу 2.1, визначити стрілу провисання проводу АС - 240/32 нормальної конструкції для середньорічних експлуатаційних умов роботи. Провід буде змонтований на уніфікованих двоколових вільностоячих сталевих опорах 220 кВ.
Вихідні дані і пояснення
Відповідно до технічних даними (табл. 2.1), провід АС-240/32 нормальної конструкції має поперечний переріз алюмінієвого провідника Fс = 238 мм. а сталевого сердечника - Fc = 43,1 мм. Відношення площ поперечних перерізів алюмінію і сталі, що позначається,. Відповідно до [13, стр. 324, 325, табл. 2.5.7]
для сталеалюмінієвих проводів перетином 120 мм 2 і більше при m = 6,11-6,25 допустиме напруження при середньорічній температурі # 963; д = 8,7 даН / мм. Среднеексплуатаціонний умови роботи проводу характеризуються навантаженням на провід # 947; 1 = 0,35 · 10-2 даН / м мм2.
За умовою завдання провід буде змонтований на уніфікованих двоколових вільностоячих сталевих опорах 220 кВ. Марка опори П220-2 [6, стор. 40, табл. 1.34]. Для даного типу опор допустимими є проміжні прольоти в межах l = 470-345 м. Для вирішення прикладу візьмемо 470 м.
Рішення
Так як довжина проміжного прольоту менше ніж 800 м, то стрілу провисання проводу визначимо за формулою 2.17, тоді
Визначення стріли провисання проводу при перетині повітряними лініями електропередачі водних перешкод і інженерних споруд
При проектуванні повітряних ліній потрібно визначати відстань по вертикалі від проводу до різних перетинаються інженерних споруд або водних перешкод, щоб перевірити, чи буде дотримуватися допустимий розмір від нижчої точки кривої провисання проводу до споруди або перешкоди [3, 11, 13, 14]. Як правило, в цих випадках буває відома тільки висота точок підвісу проводу на опорах (точки А і В), а висота нижчої точки кривої провисання проводу Про невідома. Так як місцезнаходження точки О, яка одночасно є початком координат невідомо, то приймають систему координат з початком у фіксованій точці, наприклад, в одній з точок підвісу, яка розташована вище (точка А на рис. 2.14). Ось X направляють в сторону прольоту, а вісь Y - вниз, паралельно дії навантаження, як це показано на рис. 2.14.
Так як висоти точок підвісу А і В різні, а місцезнаходження точки Про невідомо, то умова статичної рівноваги порушено. У цьому випадку крім тяжіння H необхідно врахувати вертикальну реакцію V, паралельну осі Y, але протилежну їй за напрямком.
Незалежно від різниці в висотах точок підвісу дроти вертикальна реакція залежить тільки від ваги проводу, рівномірно розподіленого по всій його довжині, і дорівнює вазі, помноженому на половину довжини прольоту:
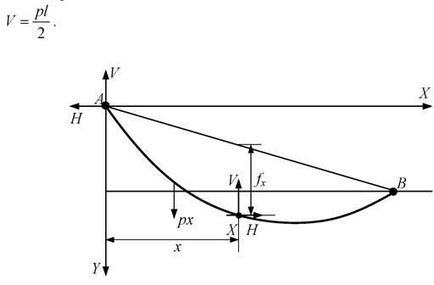
Рис.2.14. До визначення координат будь-якої точки проводу щодо початку, прийнятого у верхній точці підвісу
Складемо рівняння моментів всіх зовнішніх сил, прикладених е довільній точці Х з координатами (х; у) (на рис. 2.14 точка Х знаходиться в середині прольоту) з урахуванням зосередженої сили від власної маси дроти рх, що діє в середині даної ділянки:
(2.22)
Шуканої величиною в рівнянні (2.22) є fx. Вирішуючи його щодо шуканої стріли провисання, отримаємо:
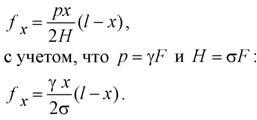
(2.23)
(2.24)
У разі, якщо точка В виявиться вище точки А, необхідно за початок координат прийняти точку В і змінити напрямок осі Х, направивши її в сторону прольоту, тоді рівняння 2.24 непорочно збережені зміни.