Побудова архітектурних обломів

Облом або мулюри - це найпростіші криві, з яких складаються профілі ордера.

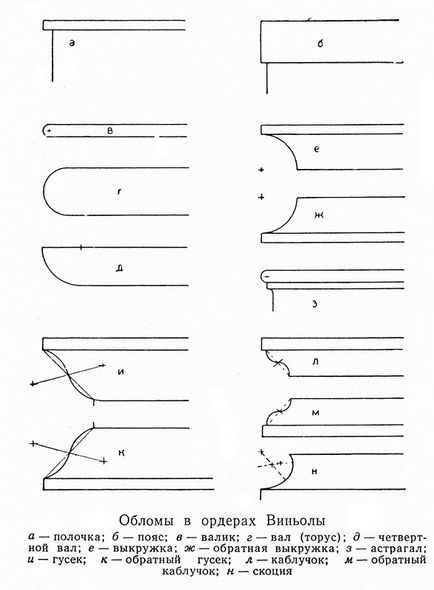
Поличка - дуже малий плоский пояс.

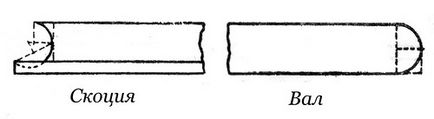
Вал - профіль, окреслений півколом; в плані - завжди коло. Валик або астрагал - малий профіль напівкруглою-опуклий або окреслений іншої подібної кривої.

1. АВ = 7 парт. ВС = 5 п.Ab = 6 ½ п. Aa = 3 п. Cc = ce = ed = 3 п.cd = 5 п.аf = 3 п .;
2. Перпендикуляр з середини прямої ef дає точку g, що є центром дуги.
3. Отже, для побудови валу (в разі 3) знадобилося 3 центру: точка b для дуги Aa, точка g для дуги ad і точка e для дуги dc.

Викружки - облом з увігнутою кривою; його застосовують для з'єднання інших обломів

1. Точка В є центр дуги AC
2. Перпендикуляр до AC, що проходить через її середину, дає DE. Точка перетину O. Перетин перпендикулярів, що проходять через середини ліній oC і ОА, в точці F утворює центр дуги CoA.
3. ABD рівносторонній трикутник; CB ділимо на 5 рівний частин; B - центр дуги EF; пряму EF продовжуємо до точки G. Точка A є центр дуги GH. Пряму GH продовжуємо до перетину з продовженням лінії CB в точці I. H - центр дуги AG; I - центр дуги GE.

четвертний вал

Четвертний вал - облом окреслений чвертю кола або іншої подібної кривої.

1. B - центр дуги AC.
2. Перпендикуляр, що проходить через середину AC, є DE. Точка F - точка перетину. Перпендикуляри до ½ AF і FC дають точку G - центр дуги AFC. (Див. 2). G - центр дуги CFo, H - центр дуги oI.

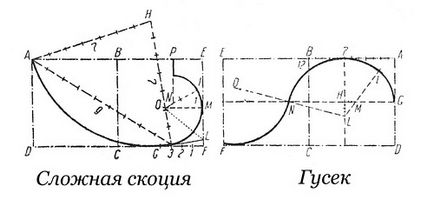
Гусек - хвилеподібний облом з увігнутою верхньою частиною і опуклою нижньою.

1. 1.2. 3. ABCD є квадрат.1.2. Квадрат АBCD розділений на 4 рівних квадрата.Точкі G і F - центри дуг DE і ЕВ.
2. Перпендикуляр, що проходить через середину DE, дає точки a і b. O - точка перетину. Перпендикуляр до ½ Еo дає точку F - центр дуги EoD.
3. DG є ½ DC; DEFG є квадрат; Е - центр дуги FbD; EG - діагональ квадрата; o - точка перетину.
4. Перпендикуляр c ½ oD дає точку H - центр дуги FoD; Hl паралельна DB; перпендикуляр до ½ Hl дає M - центр дуги FB.

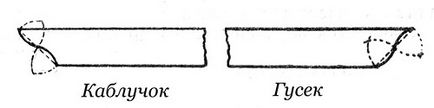
Каблучок - верхня частина випукла, нижня - увігнута.

1. 1.2.3. 4. C лежить на ½ АВ.
2. BCD рівносторонній, вигнутий трикутник.
3. AB розділимо на 6 рівних частин; DCE рівносторонній трикутник (сторона якого - 2 п.) Продолжненіе прямий DE дає точку F - центр дуги GD. Точка E - центр дуги DC.
4. Перпендикуляр до ½ BC дає точку Е - центр дуги BC.
5. (Див. 1). DE - перпендикуляр, що проходить через середину BC; точка про - точка перетину. До ½ oC відновлюємо перпендикуляр; точка перетину - F; центр дуги CoB.

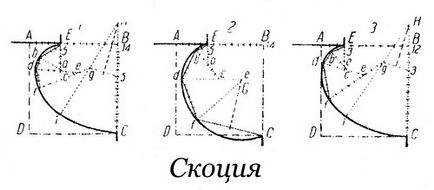
Скоція - профіль у вигляді «С», зазвичай розташований між двома поличками.

1. AB і BC розділені на 14 п. Кожна; 5 ab - рівносторонній трикутник зі стороною, що дорівнює 4 п .; bc = 6 п .; bd = 2 п .; de = 7 п .; df = 3 п .; fg = 9 п. Перпендикуляр до 1 / g 5 дає H центр дуги iC. Отже для побудови скоція (випадок 1) знадобилося 5 центрів: a - для дуги Eb, з - для дуги bd, e - для дуги df, g - для дуги Eb, H - для дуги iC.
2. АВ розділимо на 14 п. 5а = 3 п .; 5b = 2 п .; be = 6 п .; bd = 5 п .; de = 9 п. df = 7 п. Перпендикуляр до ½ fC дає G - центр дуги fC. Отже, для побудови скоція (випадок 2) знадобилося 4 центри: a - для дуги bE; с - для дуги db, e - для дуги df і G - для дуги fC.
3. AB і BC розділимо на 12 п. Кожна. AE = 3 п .; Ea = 2 ½ п .; Eb = 2 п .; bc = 3 ½ п .; bd = 2 п .; de = 5 ½ п .; df = 5 п .; fg = 9 п. Перпендикуляр до ½ g 3 дає H центр дуги iC.

складна скоція

1. ABCD = BDFC; CG є ½ FC; G3 - ½ GF; АВ розділена на 9 п .; AH = H3 = 7 п. 3L препендікулярно H3. lO бісектриса кута 3LM. O - центр дуги 3MP; МL = 1 п .; lN =. п .; Np - перпендикуляр.
2. ABCD = BEFC; BA розділене на 12 п .; G лежить на ½ AD. GH і 7H половини осей овалів (7IG - крива овалу). M - центр дуги IG; L - центр дуги I7N; NO = LN; O - центр дуги NF.

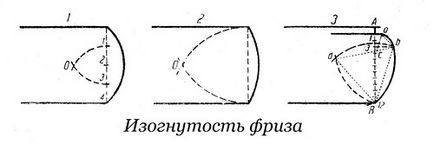
вигнутість фриза

1. Висота розділена на 4 частини (4 п.); дуги 1-3 дають центр O кривої.
2. Точка О - центр кривої.
3. Висота AB розділена на 12 п .; Al = la = 1 п .; 3b = 2 п .; ab - сторона рівностороннього трикутника abc; bB - сторона рівностороннього трикутника bBd; c і d - центри дуг ab і bB.

Схожі статті

• 1 Архітектурні обломи