Перетворення двійкового коду в двійково-десятковий

Головна | Про нас | Зворотній зв'язок
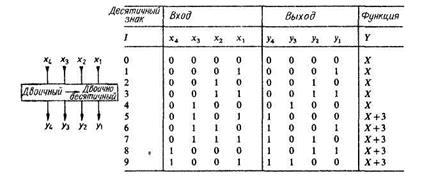
При перетворенні чотирирозрядний двійкового числа в двійковій-десяткове: числа до 9 включно залишаються без зміни.
Числа понад 9, що представляють собою псевдотетради, піддаються корекції.
Двійкові числа, що містять більше 4 розрядів, можна перетворити
аналогічним чином. Для цього двійкове чис-ло, починаючи зі старшого розряду, «вдві-гается» справа наліво в двійковій-десятич-ву розрядну сітку, як показано на рис. 6. Коли будь-яка одиниця пере-Сека кордон між двійковій-десяткових-ми розрядами, виникає помилка. Действи-тельно, в разі довічного числа розряд-ве значення цієї одиниці при зсуві збільшується з 8 до 16, тоді як для двійковій-десяткового числа воно зростає від 8 до 10. Тому на цьому етапі двійковій-десяткове число як би зменшується на 6. Отже, для корекції необ-ходимо додавати 6 до числа в усіх ви-чаях, коли одиниця перетинає кордон ме-жду двійковій-десятковими розрядами. До числа десятків треба додати 6, якщо одиниця перейде в розряд сотень, і т.д.
Складений таким чином двійковій-де-сятічное число має правильне значення, проте воно може ще містити псевдо-тетради. Щоб цього не було, возникаю-щие псевдотетради коректують непо-безпосередніх після кожного кроку зсуву, додаючи 6 до відповідної декаді з перенесенням 1 в наступну.

Мал. 6. Перетворення двійкового коду в двійково-десятковий,
в якості прикладу взя-то число 218.
Отже, обидві зазначені корекції виробляються за допомогою однієї. і тієї ж операції, а саме шляхом додавання 6.
Замість того щоб додавати після зсуву 6, з тим же успіхом можна перед зрушенням додавати 3. Необхідність той-який корекції можна також визначити перед зрушенням. Якщо значення тетради менше або дорівнює 4 = - 01002. то при після-дме зсуві не відбудеться переходу одиниці через кордон між декадами і не виникнуть псевдотетради. Таким чином, таку тетраду можна буде без змін зрушувати вліво. Якщо значення тетради перед зрушенням дорівнює 5, 6 або 7, то також не відбудеться переходу одиниці че-рез кордон, оскільки старший розряд ра-вен нулю. Однак при цьому виникнуть псевдотетради: десять, дванадцять, чотири-надцять або одинадцять, тринадцять, п'ят-надцять (в залежності від того, чи буде в молодший розряд зрушать нуль або оди-ка). Отже, в цих випадках необ-ходима корекція псевдотетрад шляхом додавання 3 перед зрушенням.
Якщо значення тетради становить 8 або 9, необхідно коригувати пере-хід одиниці через кордон між декада-ми. Тому після кожного зсуву по-є правильні тетради 6 або 7 або 8 або 9. При такій корекції псев-дотетрад отримане значення кожної тетради не може бути більше 9. Цим ис-вичерпується всі можливості, і ми напів-чим таблицю корекції 2 .
Поряд з подібним способом реалі-ції перетворення кодів за допомогою схем з пам'яттю можна використовувати комбінаційні схеми, в яких опера-ція зсуву проводиться за допомогою з-ответствуй логіки. Ця схема предста-тичних на рис. 7. Замість зсуву числа справа наліво тут зліва направо
Таблиця 2. Таблиця перемикань коригується елементів-та
для перетворення двійкового коду в двійково-десятковий
«Сдвігатель» кордону двійковій-десяткових раз-рядів, а кожна отримана тетрада кор-ректіруется відповідно до табл. 2. Отже, для «зсуву» розрядної сітки за допомогою комбінаційної схеми на кожну декаду і кожен крок зсуву необхідно по одному коригуючого елементу. Ця схема дещо спрощує-ся, якщо виключити ті коригувальні елементи, до входів яких підключено менше трьох двійкових розрядів, оскільки
в цьому випадку корекція не потрібна. На рис. 7 приведена комбінаційна схема для перетворення 8-розрядної двійковій-го числа. Цю схему легко поширити на будь-яке число розрядів. Елементи, які не ис-пользуемие для перетворення 8-розряд-ного числа, показані пунктиром. З по-міццю записаних тут чисел можна простежити за процесом перетворення коду для прикладу, наведеного
Коригувальні комбінаційні схеми поставляються в вигляді программи-руемих виробником мікросхем ПЗУ їм-кісткою 32 байта. В одному корпусі разме частішають три коригувальних елемента (рис. 8). Так як, згідно рис. 7, молодший розряд не подається на коректив-рующую схему, то за допомогою однієї ІС можна перетворити 6-розрядний двоіче-ве число, а для 8-розрядного числа потрібні три таких ІС.