Освітній портал ТГУ
Головними осями називаються такі осі координат, щодо яких відцентровий момент інерції дорівнює нулю.
Користуючись теоремою про моментах інерції при повороті осей координат, знайдемо положення головних осей:
Розділимо кожне з доданків на:
Отриманий кут a відкладається проти годинникової стрілки відносно початкової системи координатних осей.
Моменти інерції в головних осях координат приймають екстремальні значення. Для доказу візьмемо першу похідну від по a і прирівняємо її до нуля:
тобто серед безлічі осей, які можна провести через задану точку саме щодо головних осей осьові моменти інерції приймають екстремальні значення.
Взаємно перпендикулярні осі, з яких хоча б одна збігається з віссю симетрії, є головними осями.
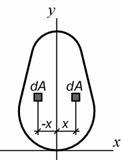
Очевидно, що кожної елементарної майданчику, розташованому по одну сторону від осі симетрії, відповідає точно така ж по іншу сторону, для якої твір координат відрізняється тільки знаком. Таким чином, відцентровий момент інерції
Головні осі можна провести через будь-яку точку перетину, проте найбільший інтерес представляють головні осі, що проходять через центр ваги (головні центральні осі).
Цікаво, що, якщо два головних центральних моменту інерції перерізу рівні між собою (Jx = Jy. Jxy = 0), то, відповідно до теореми про моменти інерції при повороті осей координат, у цього перетину будь-яка центральна вісь є головною і всі головні центральні моменти інерції однакові. У деяких випадках такі фігури легко вказати: вони мають більше двох осей симетрії (рівносторонній трикутник, квадрат, інші правильні багатокутники, коло, кільце).