Основи розрахунку залізобетону
46. Що означають 100 діб для переднапруженого залізобетону?
Це термін з моменту виготовлення конструкції, протягом якого вона повинна бути завантажена проектної навантаженням. Справа в тому, що формули для визначення втрат напруг від усадки і повзучості бетону виведені виходячи з цього терміну. Якщо конструкція завантажена в більш ранньому віці, то це навіть добре: менше втрати напруг, більше сила обтиску, вище жорсткість і тріщиностійкість. Якщо конструкція пролежала на складі більше 100 діб, то втрати напруги перевищать розрахункові значення. Таку конструкцію необхідно перерахувати (а іноді і випробувати) і, можливо, доведеться використовувати під більш низьку навантаження.
Перерахунок починається з того, що проектні втрати від усадки і тривалої повзучості множать на коефіцієнт jl = 4t / (100+ 3t), де t - фактичний вік вироби в добі. Далі з урахуванням зміненої сили обтиску знову перевіряють жорсткість і тріщиностійкість.
47. Що таке коефіцієнт точності натягу?
У виробництві будь-яких виробів можуть бути неточності, які заздалегідь враховують і допускають в обмежених розмірах. Однією з них при виготовленні попередньо напружених виробів є похибка в натягу арматури, що викликає збільшення або зменшення величини попереднього напруження ssp в порівнянні з розрахунковою - це враховується умноженіемssp на коефіцієнт точності натягу gsp. Якщо несприятливий вплив на роботу конструкції надає знижене значення ssp (наприклад, на утворення тріщин в зоні, розтягнутої при експлуатації), то gsp <1; если повышенное (например, на прочность в стадии обжатия), тоgsp> 1. При підрахунку втрат напруг, ширини розкриття тріщин і прогинів допускається приймати gsp = 1. Значення gsp наведені в Нормах проектування.
Не слід плутати gsp з допустимим відхиленням p. Якщо p використовують при призначенні проектної величини попереднього напруження, то gsp - при розрахунку безпосередньо самих перетинів.
48. Чому становище сили обтиску P не завжди збігається з центром ваги напруженої арматури?
Усадка і повзучість бетону викликають не тільки втрати напружень в напруженій арматурі, а й стискають напруги в ненапружуваній арматурі ss і ss' (рис. 22). В результаті, після других втрат сила обтиску Р з зусилля натягу арматури перетворюється в рівнодіюча всіх внутрішніх сил в перерізі: Р = sspAsp-ssAs-ss'As', а її ексцентриситет відносно центра ваги (ц.т.) перетину дорівнює
еор = (sspAspysp-ssAsys + ss'As'ys') / P. тобто не збігається з ysp. Напруження ss і ss' в ненапружуваній арматурі визначають за тими ж формулами Норм, що і втрати напруги s8 і s9 в напруженої
49. Що таке наведені перетину?
Бетон і арматура, хоча і працюють спільно, але мають різні модулі пружності: при однакових деформаціях в них виникають різні напруги. Щоб підрахувати їх, перетину призводять до одного матеріалу (зазвичай до бетону) через коефіцієнт приведення a = Еs / Eb. де Еs і Еb - модулі пружності арматури і бетону (початковий). Такі перетину називають наведеними. Пояснимо прикладом.
Потрібно визначити напруги в бетоні переднапруженого елемента, обжатого осьовою силою Р = sspAsp. де Аsp - площа перерізу напруженої арматури. Після обтиску елемент пружно коротшає на величину Dl. або eb = Dl / l (рис. 23, а), причому разом з бетоном коротшає і напружена арматура: Desp = eb. Зусилля в ній падає на величину D Р = DsspAsp = DespEsAsp.
Отже, щоб обчислити напруги в бетоні при стисненні, зовсім не обов'язково враховувати пружне вкорочення арматури і падіння в ній зусилля Р - досить первісне значення Р поділити на площу приведеного перерізу.
У більш складних випадках однієї площі недостатньо. Наприклад, щоб обчислити sbp в будь-якій точці приведеного перерізу при відцентровому обтисненні (рис. 23, б) потрібно знати статичний момент Sred (для знаходження центра ваги приведеного перерізу) і момент інерції Jred. Тоді sbp = Р / Ared ± Peopy / Jred. де y - відстань від центра ваги до цікавить точки.
50. Чим відрізняються стадії роботи звичайних і попередньо напружених залізобетонних елементів?
Розглянемо роботу центрально розтягнутого елемента (рис. 24) зі звичайною (а) і напруженої (б) арматурою. У елемента зі звичайною арматурою до додатка зовнішнього навантаження напруги відсутні (якщо знехтувати впливом усадки) - стадія 1. З додатком зовнішньої сили N в бетоні і арматурі з'явилися розтягують напруги (стадія 2), причому з умови спільності деформацій в арматурі напруження в a разів більше , ніж в бетоні: ebt = es; sbt = Ebeb; ss = Eses. звідки ss = sbtEs / Eb = asbt. У міру зростання N бетон досягає межі міцності на розтяг (sbt = Rbt), а напруги в арматурі складають ss = 2aRbt. де цифра 2 враховує подвоєння, в порівнянні з пружною частиною, деформацій в бетоні ebt до моменту його розриву (див. діаграму на рис.1). Зовнішня сила N на момент утворення тріщин (розриву бетону) складає Ncrc = = Nbt + Ns = RbtAb + 2aRbtAs = Rbt (Ab + 2aAs), де Аb і As - площі перерізу відповідно бетону і арматури. Після утворення тріщин все навантаження сприймається арматурою (стадія 3): N = ssAs.
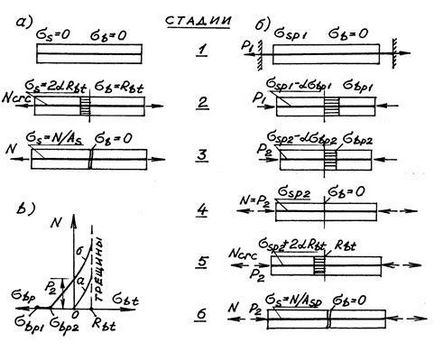
У елемента з напруженою арматурою на стадії 1 арматура натягнута і закріплена на упорах, в ній проявилися перші втрати (крім втрат від швидкоплинної повзучості). Стадія 2 - натяг відпущено, бетон обжатий силою Р1 = ssp1Asp. напруги в ньому sbp1 = P1 / Ared. напруги в арматурі зменшилися за рахунок швидкоплинної повзучості і пружного укорочення бетону і склали ssp1 -asbp1. Стадія 3 - проявляються другі втрати, сила обтиску зменшується до величини Р2. напруги в бетоні - до величини sbp2 = P2 / Ared. а напруги в арматурі - до величини ssp2 -asbp2. Стадія 4 - прикладена зовнішня навантаження N. у міру зростання якої напруги в бетоні sbp2 падають до нуля, а напруги в арматурі ростуть на величину asbp2 - сила обтиску бетону Р2 погашена, елемент повертається у вихідне положення на стадії 1, але з одним суттєвим застереженням: в бетоні проявилися деформації усадки і повзучості, а в арматурі безповоротно втрачена частина напружень. Умова рівноваги: N = P2 = ssp2Asp. Стадія 5 - бетон розтягується до напружень sbt = Rbt при навантаженні Ncrc.