Огляд методів виявлення характерних точок
Матеріал з Вікі-фотограмметрії
Характерна точка (точка інтересу) - точка зображення, що володіє високою локальної інформативністю. Як чисельної міри інформативності пропонуються різні формальні критерії, звані операторами інтересу. Оператор інтересу повинен забезпечувати досить точне позиціювання точки в площині знімка. Необхідно також, щоб положення точки інтересу мало достатню стійкість до фотометричним та геометричних спотворень зображення, що включає нерівномірні зміни яскравості, зрушення, поворот, зміна масштабу, спотворення ракурсів.
Виділення характерних точок на зображенні є початковим етапом в завданні ототожнення. Основною перевагою використання характерних точок для задач виявлення є відносна простота і швидкість їх виявлення. Крім того, на зображеннях не завжди вдається виділити інші характерні риси (чіткі контури або області), в той час як характерні точки в переважній більшості випадків виділити можна.
Найбільш простим прикладом характерних точок служать локальні екстремуми яскравості і максимуми середньоквадратичного відхилення (СКВ) яскравості. У багатьох простих випадках, коли радіометричні й спотворення ракурсів відсутні, таких точок буває цілком достатньо для прив'язки зображень. У більш складних випадках необхідно виявити на зображенні точки, використовуючи не тільки яскравості, але і стійкі до геометричних спотворень ознаки. Одним з найбільш інформативних особливостей будь-якого зображення є кути, які повсюдно зустрічаються на зображеннях будівель (кути дахів, вікон), вони також присутні на аерофотознімки природних ландшафтів.
Розглянемо фрагмент \ (U \) зображення \ (I (x, y) \) з центром в точці \ ((u, v) \), і його копії, зрушені на величину \ ((x, y) \).
Для кожної точки фрагмента можна обчислити зважений квадрат різниці між зрушеним і вихідним фрагментом, і розглянути функцію:
Функція \ (I (u + x, v + y) \) може бути розкладена в ряд Тейлора в околиці центру \ ((u, v) \), що дозволяє перейти від (1) до вираження:
де. \ (I_x \) і \ (I_y \) - приватні похідні яскравості в горизонтальному і вертикальному напрямках.
Вираз (2) можна записати в матричному вигляді: \ [S (x, y) \ approx (x y) M \ left (\ begin x \\ y \ end \ right), \]
де. \ (M = \ sum_ \ left [\ begin I_x ^ 2 I_xI_y \\ I_xI_y I_y ^ 2 \ end \ right] (3) \) - матриця локальної структури.
Як ваговій функції \ (w (u, v) \) зазвичай використовується функція Гаусса. Кут характеризується великими змінами функції \ (S (x, y) \) по всіх можливих напрямах \ ((x, y) \), що еквівалентно великим по модулю власним значенням матриці \ (M \).
Звідси випливає ряд висновків:
1. Якщо власні значення \ (λ_1 \) і \ (λ_2 \) близькі до нуля, то піксель з центром в \ ((x, y) \) не є точкою інтересу, оскільки він лежить в однорідній області.
2. Якщо \ (λ_1 \ approx 0 \), а \ (λ_2 \) приймає велику по модулю значення, то піксель \ ((x, y) \) належить краю.
3. Якщо обидва власних значення великі і приймають позитивні значення, то піксель \ ((x, y) \) є кутом.
Більшість операторів детектування кутів засновані на властивостях матриці \ (M \). В [4] для цього найменше власне значення матриці \ (M \) порівнюється з порогом. В [3] Харрісом і Стефенсом було запропоновано використовувати міру відгуку кута:
де. \ (K \) - емпірично знайдений параметр порядку 0,04-0,06, а \ (det (M) \) і \ (tr (M) \) - визначник і слід матриці.
При негативному відгуку точка класифікується як потрапила на край; при відгуку, близькому до нуля, точка вважається потрапила в «плоску» область. При великих позитивних значеннях \ (z (x, y) \) вважається, що точка є кутом, так як в ній яскравість сильно змінюється в усіх напрямках. Детектор Харріса (4) інваріантний до обертання і зсуву зображення, а також до зсуву і рівномірному лінійному зміні яскравості.
Описані детектори, хоча і називаються детекторами кутів, знаходять не власне кути, а будь-які ділянки зображення, в яких є велика зміна градієнта в усіх напрямках при заданому масштабі. Детектори достатньо швидкі, оскільки зводяться до диференціювання яскравості зображення, підсумовування похідних яскравості в локальній околиці кожної точки і знаходженню заходи відгуку кута. Крім детектора Харріса існують інші методи виявлення кутів, що дозволяють знаходити кути залежно від масштабу зображення. Найбільшу популярність отримали детектори SIFT [5] (scale-invariant feature transform - масштабно-незалежне перетворення особливостей) і його прискорений варіант SURF [6] (speeded-up robust features - прискорені стійкі особливості). Детектор SIFT заснований на ідеї пошуку локальних максимумів в так званому просторі змінного масштабу (scale space). Для заданого зображення \ (I (x, y) \) простір змінного масштабу [7] є безліч значень функціоналу:
де. \ (\ Sigma> 0 \) - параметр згладжування, символ «\ (\ ast \)» означає згортку, а \ (G (x, y; σ) \) - двовимірна функція Гаусса. В [5] розглядаються зрізи простору змінного масштабу, що відрізняються постійним позитивним множником \ (k \) (рис.1).
Як точок інтересу пропонуються точки, відповідні локальним екстремумів функції:
\ [D (x, y; \ sigma) = L (x, y; k \ sigma) - L (x, y; \ sigma). (6). \]
Для отримання \ (S \) зрізів простору змінного масштабу обчислюється згортка вихідного зображення з ядром Гаусса з послідовно змінюваних параметром згладжування \ (\ sigma_0, k \ sigma_0, ..., k ^ S \ sigma_0 \). Далі знаходяться локальні екстремуми функції \ (D (x, y, \ sigma) \). Для цього значення функції \ (D (x, y, k ^ i \ sigma_0) \) в кожній точці \ ((x, y) \) порівнюється зі значеннями в восьми сусідніх пікселях при тому ж значенні параметра масштабу, а також в 18 -ти сусідніх пікселях, що належать попереднього і подальшого зрізах простору змінного масштабу. Локальні екстремуми, в яких значення \ (| D (x; \ sigma) | \) не перевищує деякий заданий поріг, відкидаються. Потім будується матриця \ (H \) друге приватних похідних (гессіан) функції \ (D (x, y, \ sigma) \). Якщо величина \ (tr (H) ^ 2 / det (H) \) менше деякого порога, то точка вважається характерною.
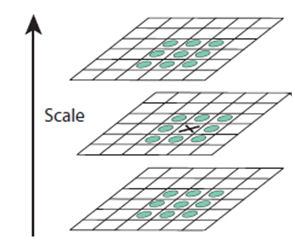
Мал. 1. Схема побудови детектора SIFT
Детектор SURF [6] використовує ту ж ідею простору змінного масштабу, що і детектор SIFT, але функція Гаусса в вираженні (5) наближається прямокутним фільтром 9 × 9. На рис.2 показані фільтри для отримання приватних похідних вихідного зображення \ (I (x, y) \) по \ (yy \) і по \ (xy \); при цьому зліва наводяться (обрізані) фільтри других похідних Гауссіана, а праворуч - прямокутні фільтри, що обчислюють ці похідні наближено. Згортка вихідного зображення з такими фільтрами, ваги яких є цілими числами, обчислюється дуже швидко. Далі в якості характерних точок виявляються локальні максимуми в вікні 3 × 3 × 3 функції:
Мал. 2. Фільтри для знаходження другої похідної яскравості зображення за напрямками \ (y \) і \ (xy \); а, б - фільтри Гаусса (SIFT); в, г - прямокутні фільтри з цілочисельними вагами (SURF)

Мал. 3. Пікселі, що використовуються в швидких перевірках алгоритму FAST
Список літератури
1. Moravec H. Rover visual obstacle avoidance // Proc. Intl. Joint Conference on Artificial Intelligence. - 1981. - P. 785-790.
2. Forstner W. A feature based correspondence algorithm for image matching // Intl. Archives of Photogrammetry and Remote Sensing. - 1986. - V. 26. - P. 150-166.
3. Harris C. G. Stephens M. J. Combined corner and edge detector // Proc. Fourth Alvey Vision Conference. - 1988. - P. 147-151.