Нормальний розподіл, гауссовское розподіл
Даний розподіл займає центральне місце в теорії і практиці ймовірносно-статистичних досліджень. Нехай значення досліджуваної безперервної випадкової величини формуються під впливом дуже великого числа незалежних випадкових факторів, причому сила впливу кожного окремого фактора мала і не може превалювати серед інших, а характер впливу - адитивний.
Функція щільності випадкових величин подібного типу має вигляд:
де μ і σ 2 параметри закону, що інтерпретуються як математичне очікування (середнє значення) і дисперсія даної випадкової величини.
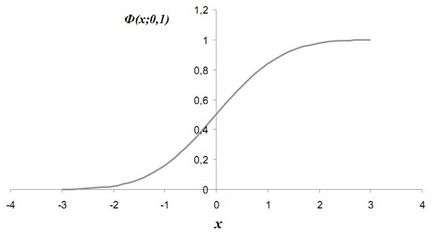
Відповідна функція розподілу нормальної випадкової величини
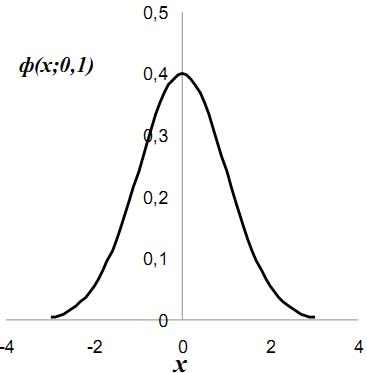
Нормальний закон з функцією щільності
(Μ = 0 і σ 2 = 1) називають стандартним. У багатьох випадкових величинах, що вивчаються в економіці, техніці, біології та в інших областях, природно бачити сумарний адитивний ефект великого числа незалежних причин.
Поняття нормального закону розподілу
Нормальний закон - це один з багатьох типів розподілу, наявних в природі, правда, з відносно великою питомою вагою практичного застосування. Повнота теоретичних досліджень, які відносяться до нормального закону, а також порівняно прості математичні властивості роблять його найбільш привабливим і зручним у застосуванні.
У разі відхилення досліджуваних експериментальних даних від нормального закону існує, принаймні, два шляхи його доцільною експлуатації: а) використовувати його в якості першого наближення; при цьому нерідко виявляється, що подібне допущення дає досить точні з точки зору конкретних цілей дослідження результати; б) підібрати таке перетворення досліджуваної випадкової величини, яке видозмінює вихідний «ненормальний» закон розподілу, перетворюючи його в нормальний.
Зручним для статистичних задач є і властивість «самовоспроізводімості» нормального закону, яке полягає в тому, що сума будь-якого числа нормально розподілених випадкових величин теж підкоряється нормальному закону розподілу.