Невизначеність «нескінченність мінус нескінченність»
Популярна невизначеність усувається трьома поширеними способами:
- приведенням вираження під знаком межі до спільного знаменника;
- множенням / поділом на поєднане вираз;
Розглянемо перший випадок, про який я ще не розповідав:
В даному межі має місце невизначеність, і загальний алгоритм вирішення нехитрий: необхідно привести вираз до спільного знаменника, а потім спробувати що-небудь скоротити:
(1) Розкладаємо знаменники на множники: в першому знаменнику виносимо «ікс» за дужки, у другому знаменнику використовуємо формулу різниці кубів. Даний крок можна було пропустити, але цим довелося б займатися потім, і, на мій погляд, розкладання на множники зручніше провести відразу ж.
(2) Наводимо вираз до спільного знаменника.
(3) Наводимо подібні доданки в чисельнику. Невизначеність трансформувалася в невизначеність, яка стандартно розкривається розкладанням чисельника і знаменника на множники.
(4) Знаменник вже розкладений на множники. Розкладаємо на множники чисельник, в даному випадку використана формула.
(5) Скорочуємо чисельник і знаменник на, усуваючи невизначеність.
Як бачите, новизни особливою і немає.
Аналогічне завдання для самостійного рішення:
Рішення і відповідь в кінці уроку
Другий вид меж з невизначеністю являє собою різницю, в якій присутні два або один корінь:
Канонічний зразок. Метод рішення детально розібраний на уроці Межі. Приклади рішень. Необхідно помножити і розділити на поєднане вираз, щоб потім скористатися формулою
Помножимо і розділимо на поєднане вираз:
Невизначеність перетворилася в невизначеність. Впізнаєте? Такі насіння ми гризли в першому розділі даного уроку.
Чисельник і знаменник одного порядку зростання, а значить, межа дорівнює кінцевому числу. Розділимо чисельник і знаменник на:
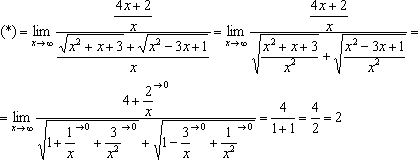
Не рідкість, коли в різниці всього один корінь, але це не змінює алгоритму рішення:
Це пара коротких прикладів для самостійного рішення.
Слід зазначити, що межі розглянутого типу не зобов'язані рівнятися кінцевого числа, цілком може вийти і нескінченність, причому, як «плюс», так і «мінус». До речі, в прикладі №13 можна подивитися на порядок зростання членів, щоб відразу з'ясувати відповідь ;-)
Іноді на практиці зустрічаються предели- «обманки», в яких невизначеності «нескінченність мінус нескінченність» немає взагалі, ось найпростіший приклад:
Таким чином, будьте гранично уважні: перед рішенням межі необхідно переконатися, що неопределённостьдействітельно є!
У заключній частині статті повернемося до незаслужено забутим чудовим меж. де розглянемо, в тому числі, третій тип меж з невизначеністю.
Метод заміни змінної в межі
Вельми ходової прийом рішення. Метод заміни змінної застосовують найчастіше для того, щоб звести рішення до першого чудовому межі. набагато рідше - до іншого чудовому межі. Розглянемо пару типових зразків:
У межі знаходиться арктангенс, від якого добре б позбутися. Логічно і дуже зручно перетворити «арк» в одну єдину букву. Проведемо заміну змінної:.
Тепер в межі потрібно висловити все інше через «те».
По-перше, з'ясуємо, куди буде прагнути нова змінна «те»: Якщо, то, іншими словами, новоспечена змінна теж буде прагнути до нуля:
Залишилося в знаменнику висловити «ікс» через «те». Для цього на обидві частини рівності «навішуємо» тангенси:
У правій частині дві взаємно зворотні функції знищуються:, звідки:
Помахи чарівної палички закінчені, решта просто:
Використовувані формули і прийоми рішення завершального етапу дуже докладно розібрані в першій частині уроку Чудові межі.
Це приклад для самостійного рішення. Зразок чистового оформлення в кінці уроку.
Ще пара цікавих прикладів на тему заміни змінної:
При підстановці одиниці в межа виходить невизначеність. Заміна змінної вже напрошується, але спочатку перетворимо тангенс за формулою. Дійсно, навіщо нам тангенс?
Зауважте, що, тому. Якщо не зовсім зрозуміло, подивіться значення синуса в тригонометричної таблиці. Таким чином, ми відразу забрали від множника, крім того, отримуємо більш звичну невизначеність 0: 0. Добре б ще й межа у нас наближався до нуля.
Під косинусом у нас знаходиться «ікс», який теж необхідно висловити через «те». З заміни висловлюємо:.
(1) Проводимо підстановку
(2) Відкриваємо дужки під косинусом.
(3) Використовуємо формулу приведення, формули приведення також можна знайти в тригонометричних таблицях.
(4) Щоб організувати перший чудовий межа, штучно домножаем чисельник на і зворотне число.
Завдання для самостійного рішення:
Повне рішення і відповідь в кінці уроку.
Це були нескладні завдання в своєму класі, на практиці все буває гірше, і, помімоформул приведення. доводиться використовувати найрізноманітніші тригонометричні формули. а також інші хитрощі. У статті Складні межі я розібрав пару справжніх прикладів =)
У переддень свята остаточно з'ясуємо ситуацію ще з однією розповсюдженою невизначеністю: