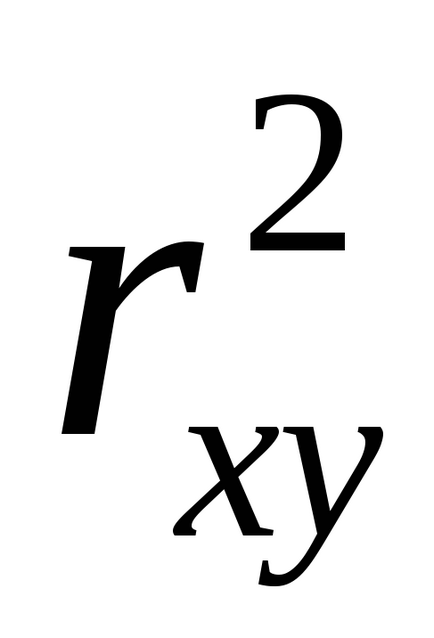необхідний мінімум

1.Дісперсія

Дисперсія - характеристика випадкової величини, яка визначається як математичне сподівання квадрата відхилення випадкової величини від її математичного очікування.

Теоретична дисперсія є мірою розкиду для імовірнісного розподілу. Вона визначається як математичне сподівання квадрата різниці між величиною

і її середнім, тобто величини

, де

- математичне очікування

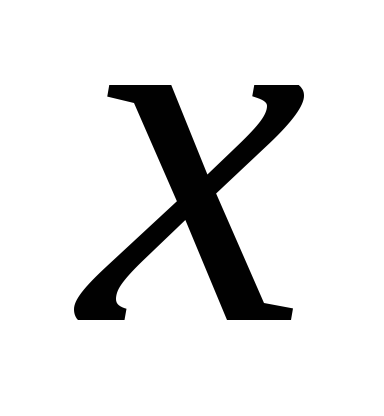
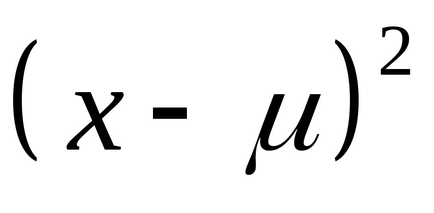
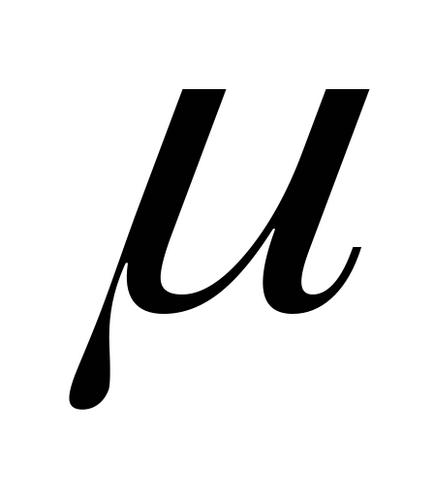
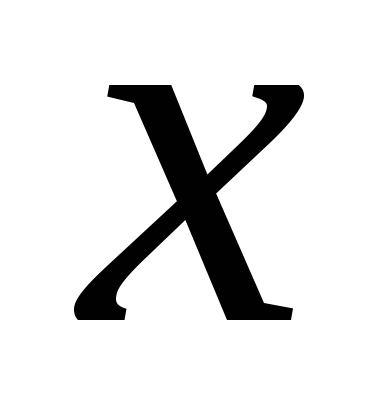
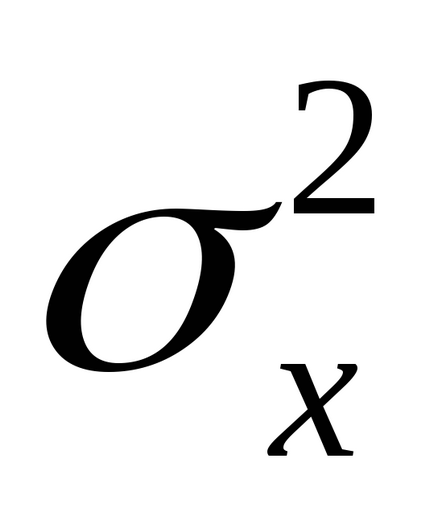
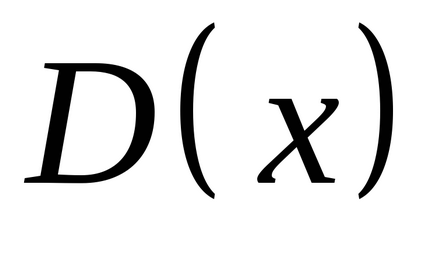
. Дисперсія звичайно позначається як

або

, і якщо ясно, про яку змінної йдеться, то нижній індекс може бути опущений:

можна отримати

середнє відхилення - настільки ж поширену міру розкиду для розподілу ймовірностей; середньоквадратичне відхилення випадкової змінної є квадратний корінь з її дисперсії.

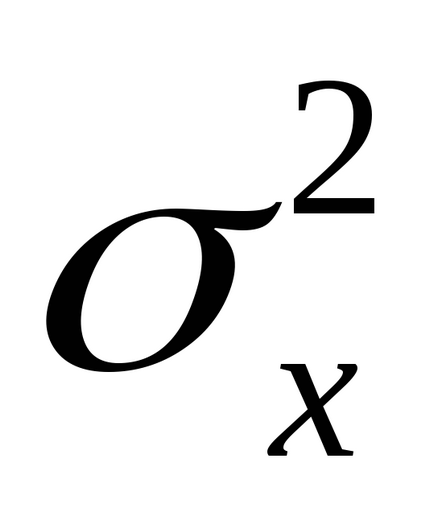
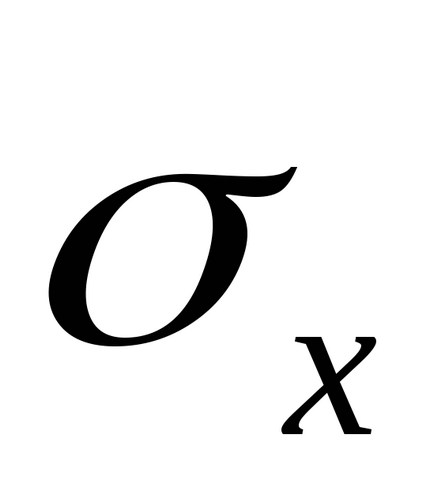
величина

характеризує частку дисперсії

, викликану впливом інших, не врахованих в моделі, факторів.

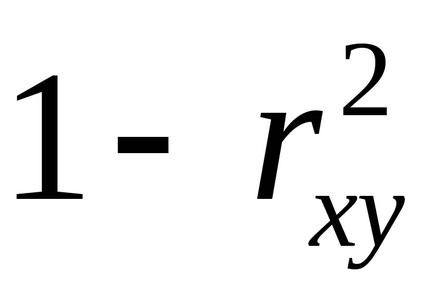
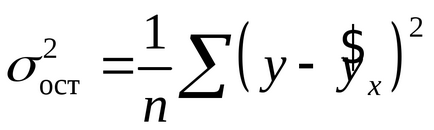
2.Мат. очікування

Математичне сподівання - сума творів значень випадкової величини на відповідні ймовірності.

Математичне сподівання дискретної випадкової величини - це зважене середнє всіх її можливих значень, причому в якості вагового коефіцієнта береться ймовірність відповідного результату. Ви можете розрахувати його, перемноживши всі можливі значення випадкової величини на їх ймовірності і підсумувавши отримані твори. Математично якщо випадкова величина позначена як

, то її математичне очікування позначається як

або

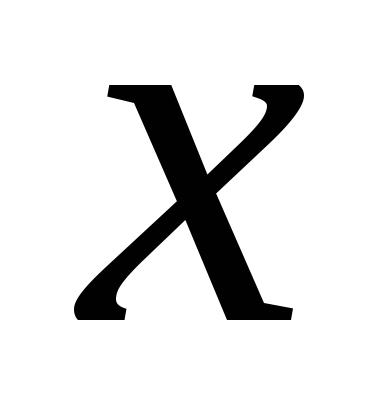
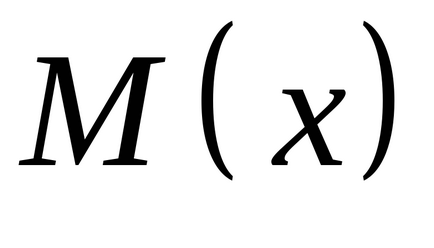
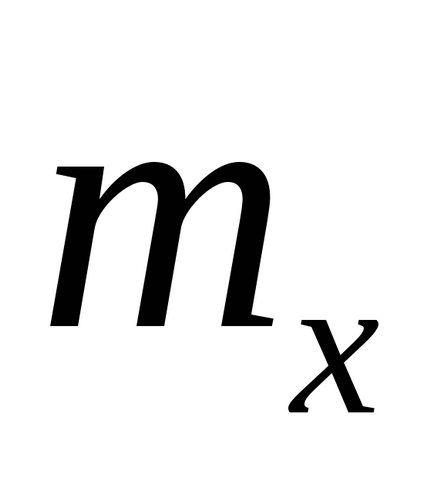
Припустимо, що

може приймати

конкретних значень

і що ймовірність отримання

дорівнює

. тоді

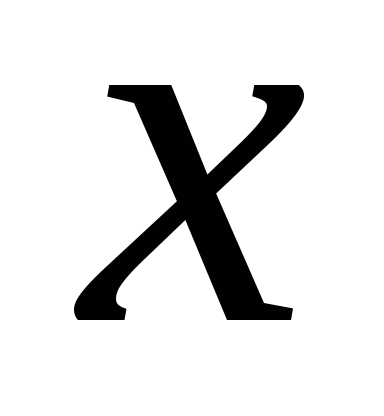
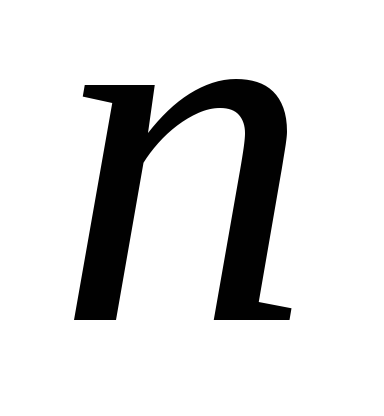
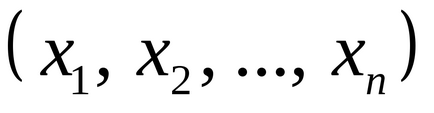
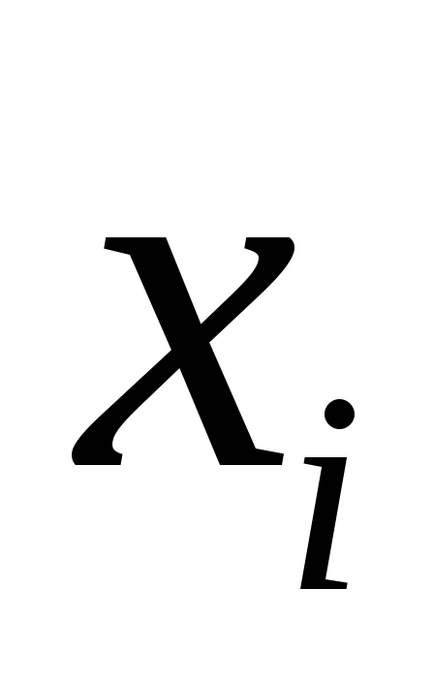
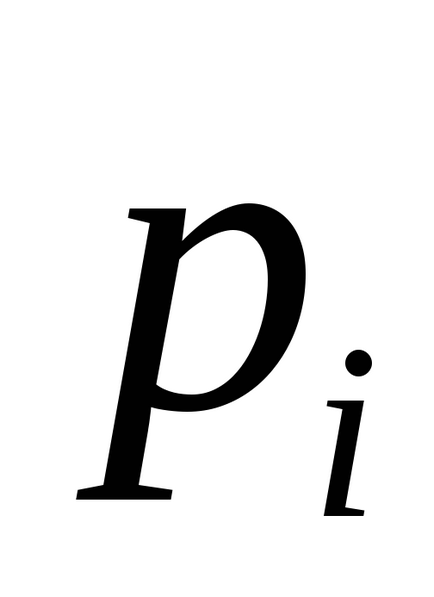
Математичне сподівання випадкової величини часто називають її середнім по генеральної сукупності. Для випадкової величини

це значення часто позначається як

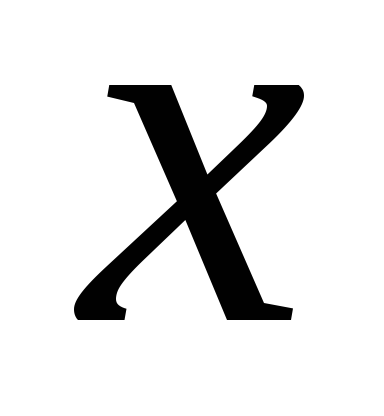
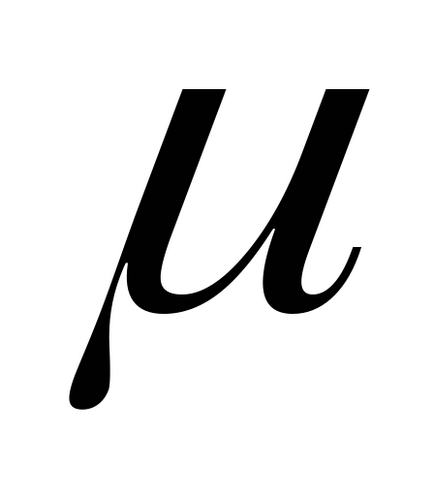
Математичні очікування функцій дискретних випадкових змінних

нехай

- деяка функція від

. тоді

- математичне очікування

записується як

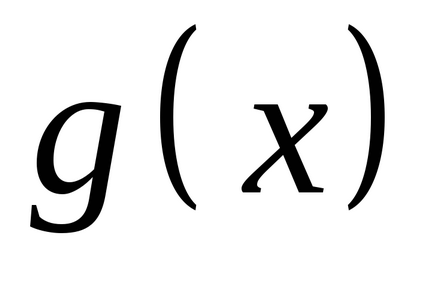
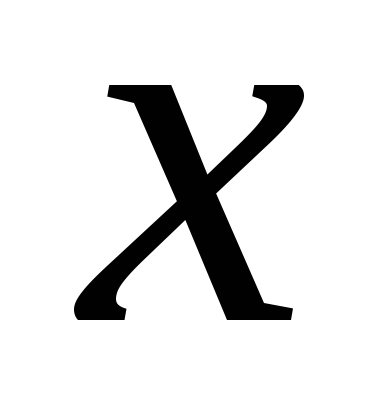
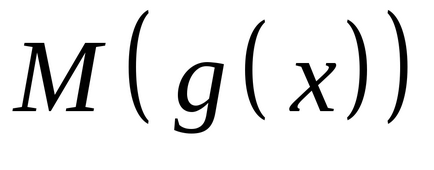
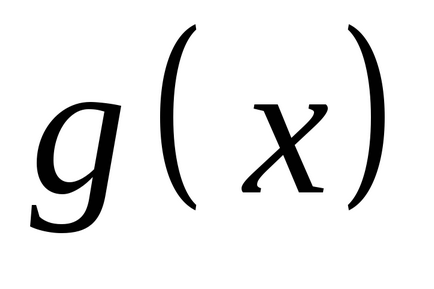
де підсумовування проводиться по всіх можливих значеннях

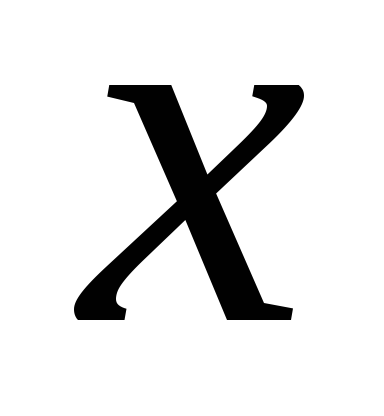
Правила розрахунку математичного очікування

Існують три правила, які часто використовуються. Ці правила практично самоочевидні, і вони однаково застосовні для дискретних і безперервних випадкових змінних.

Правило 1. Математичне сподівання суми декількох змінних дорівнює сумі їх математичних очікувань. Наприклад, якщо є три випадкові змінні

, то

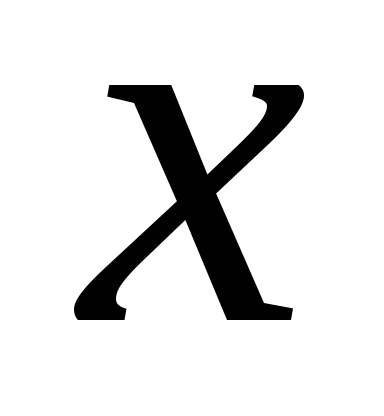
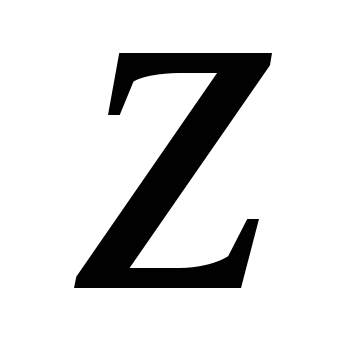
Правило 2. Якщо випадкова змінна множиться на константу, то її математичне сподівання множиться на ту ж константу. якщо

- випадкова змінна і

- константа, то

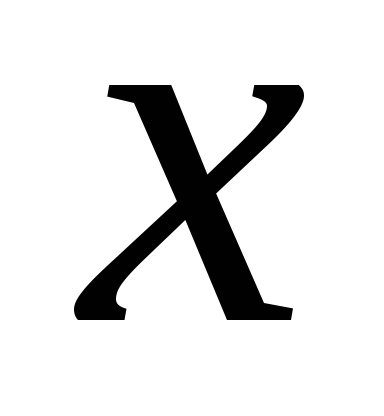
Правило 3. Математичне сподівання константи є вона сама. Наприклад, якщо

- константа, то

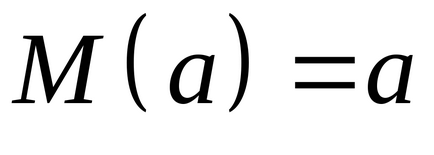
Слідство з трьох правил:

Коваріація - числова характеристика спільного розподілу двох випадкових величин, що дорівнює математичному очікуванню твори відхилень цих випадкових величин від їх математичних очікувань.

Можна скористатися наступними готовими формулами, які йдуть безпосередньо з рішення системи (1.4):

де - коваріація ознак

- дисперсія ознаки

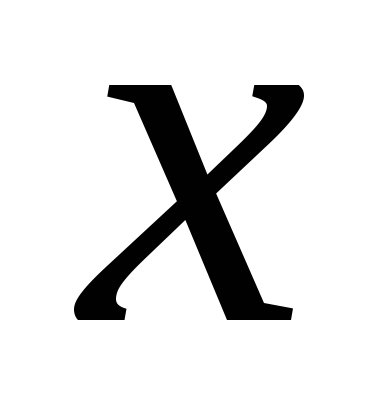
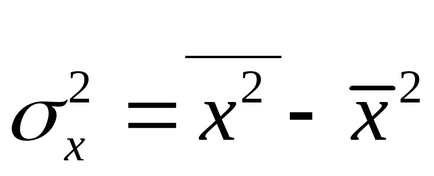
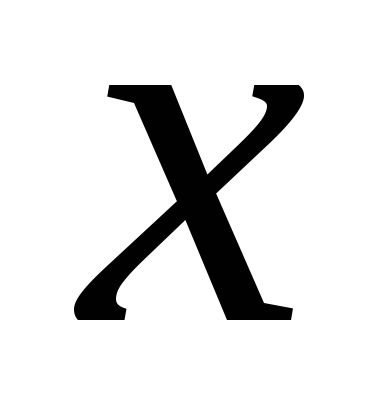
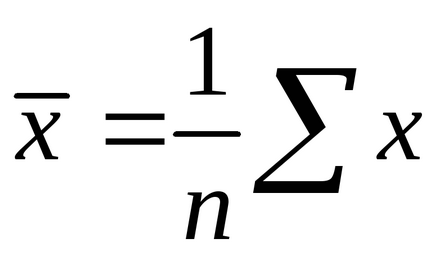
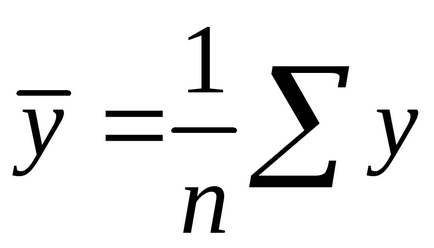
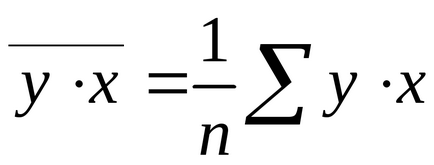
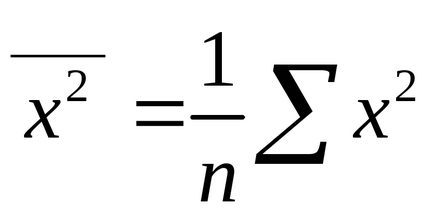
4.Корреляція

Коефіцієнт кореляції або парний коефіцієнт кореляції - це показник характеру зміни двох випадкових величин. Коефіцієнт кореляції позначається латинською буквою

і може приймати значення між -1 і +1. Якщо значення по модулю знаходиться ближче до 1, то це означає наявність сильного зв'язку (при коефіцієнті кореляції дорівнює одиниці говорять про функціональну зв'язку), а якщо ближче до 0, то слабкою.

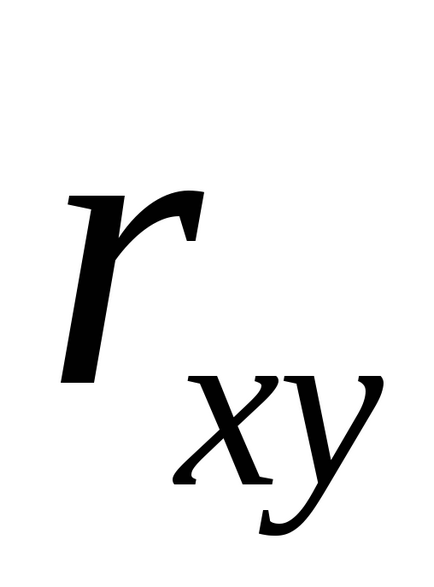
Рівняння регресії завжди доповнюється показником тісноти зв'язку. При використанні лінійної регресії в якості такого показника виступає лінійний коефіцієнт кореляції

, який можна розрахувати за такими формулами:

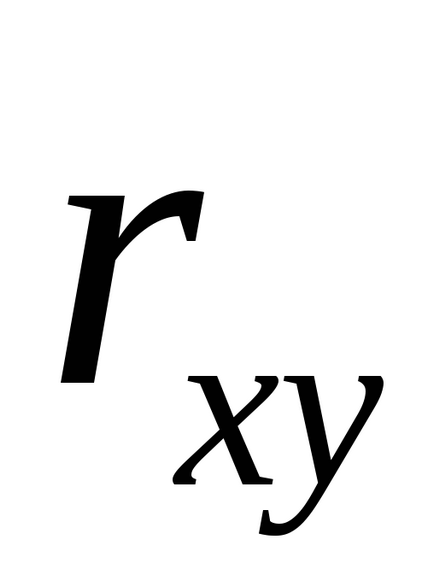
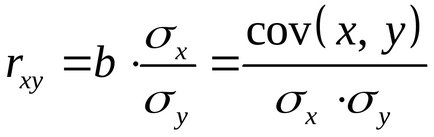
Лінійний коефіцієнт кореляції знаходиться в межах:

. Чим ближче абсолютне значення

до одиниці, тим сильніше лінійного зв'язку між факторами (при

маємо сувору функціональну залежність). Але слід мати на увазі, що близькість абсолютної величини лінійного коефіцієнта кореляції до нуля ще не означає відсутності зв'язку між ознаками. При інший (нелінійної) специфікації моделі зв'язок між ознаками може виявитися досить тісною.

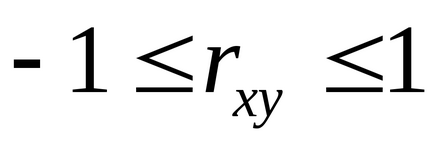
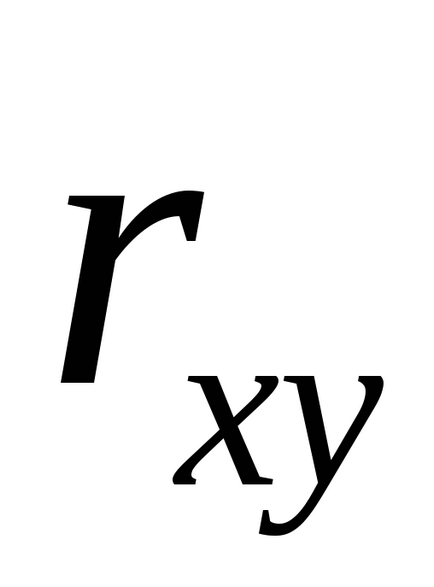
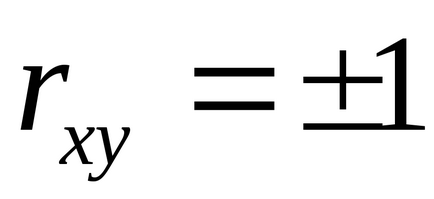
Для оцінки якості підбору лінійної функції розраховується квадрат лінійного коефіцієнта кореляції

, званий коефіцієнтом детермінації.

Схожі статті

Попередня ◈ Наступна