Матрична алгебра - транспонована матриця
Матрична алгебра - Транспонована матриця

рядків відповідно стовпцями, дає так звану транспоновану матрицю розмірності n × m:
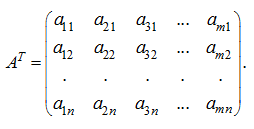
Зокрема, для вектора-строкітранспонірованной матрицею є вектор-стовпець
Основні властивості транспонованою матриці:
1) двічі транспонована матриця збігається з вихідною:
2) транспонована матриця суми матриць дорівнює сумі транспонованих матриць доданків, тобто
3) транспонована матриця твори матриць дорівнює добутку транспонованих матриць сомножителей, взятому в зворотному порядку:
Для квадратної матриці має місце очевидне рівність:
Якщо матриця збігається зі своєю транспонованою
то вона називається симетричної. З останнього рівності випливає, що симетрична матриця є квадратної, і її елементи, симетричні відносно головної діагоналі, рівні між собою:
Очевидно, що твір є симетричної матрицею, так як, використовуючи властивість 3, отримаємо:
П р и м і р. Дано матриця А і транспонована матриця:
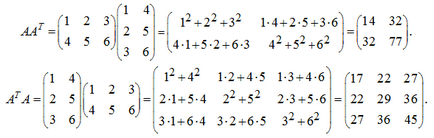
Як і слід було очікувати, отримані симетричні матриці.