Магічні квадрати з доміно
На рис. 7 показаний квадрат з 18 кісточок доміно, чудовий тим, що сума очок будь-якого його ряду - поздовжнього, поперечного або діагонального - одна і

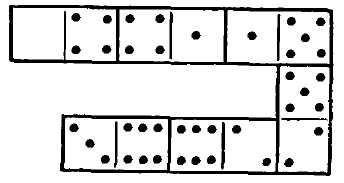
та ж: 13. Подібні квадрати здавна називаються "магічними".
Вам пропонується скласти кілька таких же 18-кісточкових магічних квадратів, але з іншого сумою очок в ряду. 13 - найменша сума в рядах магічного квадрата, складеного з 18 кісток. Найбільша сума - 23.
Прогресія з доміно.
Ви бачите на рис. 8 шість кісточок доміно, викладених за правилами гри і відрізняються тим, що число очок на кісточках (на двох половинах кожної кісточки) зростає на 1. Ряд починається з 4 і складається з наступних чисел очок:
Такий ряд чисел, які зростають (або зменшуються) на одну і ту ж величину, називається "арифметичною прогресією". У нашому ряду кожне число більше попереднього на 1; але в прогресії може бути і будь-яка інша "різниця".
Завдання полягає в тому, щоб скласти ще кілька 6-кісточкових прогресій.
ГРА В 15, АБО такенний
Загальновідома коробочка з 15 нумерованими квадратними шашками має цікаву історію, про яку мало хто з гравців підозрює. Розповімо про неї словами німецького дослідника ігор, математика В. Аренса.
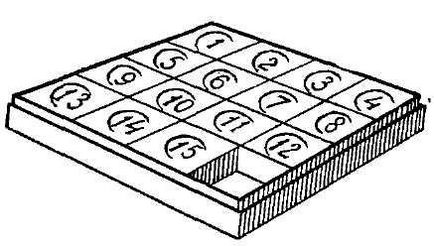
Мал. 9. Гра в 15.
"Близько півстоліття тому - в кінці 70-х років - виринула в Сполучених Штатах" гра в 15 "; вона швидко поширилася і, завдяки незліченну кількість гравців, яких вона заполонила, перетворилася на справжнє суспільне лихо.
"Те ж саме спостерігалося по цей бік океану, в Європі. Тут можна було навіть в конка бачити в руках пасажирів коробочки з 15 шашками. У конторах і магазинах господарі приходили у відчай від захоплення своїх службовців і змушені були заборонити їм гру в години занять і торгівлі . Утримувачі розважальних закладів спритно використовували цю манію і влаштовували великі гральні турніри.
Гра проникла навіть в урочисті зали німецького рейхстагу. "Як зараз бачу в рейхстазі сивочолих людей, зосереджено розглядають в своїх руках квадратну коробочку", - згадує відомий географ і математик Зигмунд Гюнтер, колишній депутатом в роки гральної епідемії.
"У 1880 р гральна лихоманка досягла, мабуть, своєї найвищої точки. Але незабаром після цього тиран був повалений і переможений зброєю математики. Математична теорія гри виявила, що з численних завдань, які можуть бути запропоновані, можна вирішити тільки половина; інша не вирішувана ніякими хитрощами.
"Стало ясно, чому інші завдання не піддавалися самим наполегливим зусиллям, і чому організатори турнірів наважувалися призначати величезні премії за вирішення завдань. У цьому відношенні всіх перевершив винахідник гри, який запропонував видавцеві нью-йоркської газети для
недільного додатку нездійсненне завдання з премією в 1000 доларів за її дозвіл; так як видавець коливався, то винахідник висловив повну готовність внести названу суму з власної кишені. Ім'я винахідника Самуель (Сем) Лойд. Він придбав широку популярність як упорядник дотепних завдань і безлічі головоломок. Цікаво, що отримати в Америці патент на придуману гру йому не вдалося. Згідно з інструкцією, він повинен був представити "робочу модель" для виконання пробної партії; він запропонував чиновнику патентного бюро завдання, і коли останній поцікавився, можна вирішити чи вона, винахідник повинен був відповісти: "Ні, це математично неможливо". "У такому випадку, - послідувало заперечення, - не може бути і робочої моделі, а без моделі немає і патенту". Лойд задовольнився цією резолюцією, - але, ймовірно, був би більш наполегливий, якби передбачив нечуваний успіх свого винаходу ". [Цей епізод використаний Марком Твеном в його романі" Американський претендент ".]
Наведемо свою розповідь винахідника гри про деякі факти з її історії:
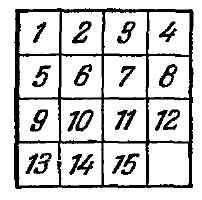
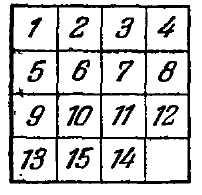
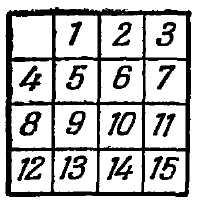
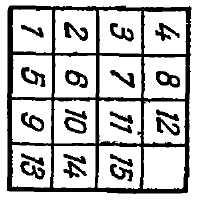
"Давні мешканці царства кмітливості, - пише Лойд, - пам'ятають, як на початку 70-х років я змусив весь світ ламати голову над коробкою з рухомими шашками, яка стала популярною під ім'ям" гри в 15 "(рис. 10). П'ятнадцять шашок були розміщені в квадратної коробочці в правильному порядку, і тільки шашки 14 і 15 були переставлені, як показано на поданій ілюстрації (рис. 11). Завдання полягало в тому, щоб, послідовно пересуваючи шашки, привести їх у нормальний стан, причому, проте, порядок шашок 14 і 15 має бути виправлений.
"Премія в 1000 доларів, запропонована за перше правильне рішення цього завдання, ніким не була заслужена, хоча все невтомно вирішували це завдання. Розповідали кумедні історії про торговців, забували через це відкривати свої магазини, про поважних чиновників, цілі ночі безперервно простоював під вуличним ліхтарем, відшукуючи шлях до вирішення. Ніхто не бажав відмовитися від пошуків рішення, так як всі відчували впевненість в очікує, їхньому успіху. Штурмани, кажуть, через гру садили на мілину свої судна, машиністи проводили поїзда повз станцій; фермери закидали свої плуги ".
Познайомимо Новомосковсктеля з усякого теорії цієї гри. У повному вигляді вона дуже складна і тісно примикає до одного з відділів вищої алгебри ( "теорія визначників"). Ми обмежимося лише деякими міркуваннями, викладеними В. Аренсом.
"Завдання гри полягає звичайно в тому, щоб за допомогою послідовних пересувань, що допускаються наявністю вільного поля, перекласти будь-яке початкове розташування 15 шашок в нормальне, т. Е. В таке, при якому шашки йдуть в порядку своїх чисел: у верхньому лівому кутку 1, направо - 2, потім 3, потім у верхньому правому куті 4; в наступному ряду зліва направо: 5, 6, 7, 8 і т. д. Таке нормальне кінцеве розташування ми даємо тут на рис. 10.
"Уявіть тепер розташування, при якому 15 шашок розміщені в строкатому безладді. Поруч пересувань завжди можна привести шашку 1 на місце, займане нею на малюнку.
"Точно так само можливо, не чіпаючи шашки 1, привести шашку 2 на сусіднє місце вправо. Потім, не чіпаючи шашок 1 і 2, можна помістити шашки 3 і 4 наіх нормальні місця: якщо вони випадково не перебувають в двох останніх вертикальних рядах, то легко привести в цю область і потім поруч пересувань досягти бажаного результату. Тепер верхній рядок 1, 2, 3, 4 приведена в порядок, і при подальших маніпуляціях з шашками ми чіпати цього ряду не будемо. Таким же шляхом намагаємося ми привести в порядок і другу рядок: 5, 6, 7, 8; легко переконатися, що це завжди досягнень жімо. Далі, на просторі двох останніх рядів необхідно привести в нормальне положення шашки 9 і 13; це теж завжди можливо. З усіх наведених в порядок шашок 1, 2, 3, 4,5,6,7,8,9 і13 надалі жодної не переміщують; залишається невелика ділянка в шість полів, в якому одне вільно, а п'ять інших зайняті шашками 10, 11, 12, 14, 15 в довільному порядку. в межах цього шестимісного ділянки завжди можна привести на нормальні місця шашки 10, 11 , 12. Коли це досягнуто, то в останньому ряду шашки 14 і 15 виявляться розміщеними або в нормальному порядку застосування ПСП , Або в зворотному (рис. 11). Таким шляхом, який Новомосковсктелі легко можуть перевірити на ділі, ми приходимо до наступного результату.
"Будь-яке початкове положення може бути приведено до розташування або рис. 10 (положення I), або рис. 11 (положення II).
"Якщо деяку прихильність, яке для стислості позначимо буквою S. може бути перетворено в положення I, то, очевидно, можливо і зворотне - перевести положення I в положення S. Адже всі ходи шашок оборотні: якщо, наприклад, в схемі I ми можемо шашку 12 помістити на вільне поле, то можна хід цей негайно взяти назад протилежними рухами.
"Отже, ми маємо дві такі серії розташуванні, що положення однієї серії можуть бути переведені в нормальне I, а інший серії - в положення II. І навпаки, з нормального розташування можна отримати будь-яке положення першої серії, а з розташування II - будь-яке положення другої серії. Нарешті, два будь-яких розташування, що належать до однієї і тієї ж серії, можуть бути перекладаються один в одного.
"Чи не можна йти далі і об'єднати ці два розташування - I і II? Можна строго довести (не станемо входити в подробиці), що положення ці не перетворювати одне в інше ніяким числом ходів. Тому все величезне число розміщень шашок розпадається на дві роз'єднані серії: 1) на ті, які можуть бути переведені в нормальне I: це - положення розв'язні, 2) на ті, які можуть бути переведені в стан II і, отже, ні при яких обставинах не переводяться в нормальне розташування: це - положення, за дозвіл яких назначаліс ь величезні премії.
"Як дізнатися, чи належить задана прихильність до першої або до другої серії? Приклад роз'яснить це.
"Розглянемо таке розташування.
"Перший ряд шашок в порядку, як і другий, за винятком останньої шашки (9). Ця шашка займає місце, яке в нормальному розташуванні належить 8.Шашка 9 варто, значить, ранеешашкі 8: таке випередження нормального порядку називають" безладом ". Про шашки 9 ми скажемо: тут має місце 1 безлад. Розглядаючи подальші шашки, виявляємо "випередження" для шашки 14; вона поставлена на три місця (шашок 12, 13, 11) раніше свого нормального стану; тут у нас 3 безладу (14 раніше 12 ; 14 раніше 13; 14 раніше 11). Всього ми нарахували вже 1 + 3 = 4 безладу. Далі, ш ашка 12 поміщена раніше шашки 11, і точно так же шашка 13 раніше шашки 11. Це дає ще 2 безладу. Разом маємо 6 заворушень. Подібним чином для кожного розташування встановлюють загальне число заворушень, звільнивши попередньо останнє місце в правому нижньому кутку. Якщо загальне число заворушень, як в розглянутому випадку, парне, то заданий розташування може бути приведений до нормального кінцевого; іншими словами, воно належить до вирішуваним. Якщо ж число заворушень непарне, то розташування належить до другої серії, т. Е. До нерозв'язною (нуль заворушень приймається за парне число їх).
"Завдяки ясності, внесеної в цю гру математикою, колишня гарячкова пристрасність в захопленні зараз абсолютно немислима. Математика створила вичерпну теорію гри, теорію, що не залишає жодного сумнівного пункту. Результат гри залежить не від будь-яких випадків, не від винахідливості, як в інших іграх, а від чисто математичних чинників, які зумовлюють його з безумовною достовірністю ".
Звернемося тепер до головоломок в цій області.
Ось кілька вирішуваних завдань, придуманих винахідником гри:
Перше завдання Лойда.
Виходячи з розташування, показаного на рис. 11, привести шашки в правильний порядок, але з вільним полем в лівому верхньому кутку (рис. 13).
Друге завдання Лойда.
Виходячи з розташування рис. 11 поверніть коробку на чверть обороту і наведіть шашки до тих пір, поки вони не приймуть розташування рис. 14.
Третє завдання Лойда.
Пересуваючи шашки відповідно до правил гри з розташування рис. 11, перетворите коробку в "магічний квадрат", а саме, розмістіть хиткі так, щоб сума чисел була у всіх напрямках дорівнює 30.
Займаючись головоломками, що відносяться до доміно і грі 15, ми залишалися в межах арифметики. Переходячи до головоломок на крокетний майданчику, ми вступаємо частково в область геометрії.
Пропоную крокетний гравцям наступні п'ять завдань.