Лабораторна робота №10 вивчення закону нормального розподілу на механічній моделі
1. Ознайомитися з нормальним (гауссовским) і максвелловським розподілом випадкових величин.
2. Ознайомитися з нормальним розподілом на механічній моделі і визначити його дисперсію і міру точності.
теоретичне введення
Випадкові явища описуються за допомогою теорії ймовірностей і підкоряються статистичним законам, що дозволяє знайти ймовірність здійснення тієї чи іншої події в серії випадкових подій, середнє значення випадкової величини, найбільш ймовірне відхилення від середнього і т.д. Всі ці характеристики визначаються законом розподілу випадкової величини - тобто залежністю ймовірності появи того чи іншого значення випадкової величини від самого значення величини.
Нехай х - деяка дискретна випадкова величина, яка може приймати s значень: х1. х2. ... хn. ... ХS. Цим значенням відповідають ймовірності: р1, р2. ... рm. ..., РS. Наприклад, рm є ймовірність того, що розглянута величина прийме значення хm. Сума всіх ймовірностей (р1 + р2 + ... + РS) є ймовірність того, що в випробуванні буде реалізовано якесь (байдуже який саме) зі значень х1. х2. ..., ХS. Ця ймовірність дорівнює одиниці.
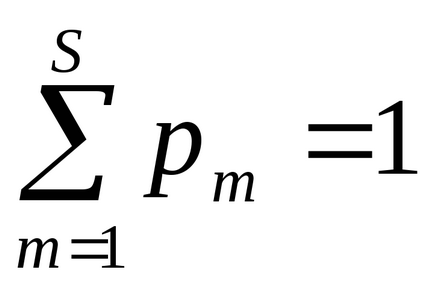
Набір ймовірностей р1. р2. ..., РS містить вичерпну інформацію про випадковій величині.
Однак у багатьох випадках на практиці знання ймовірностей необов'язково. Досить знати дві найбільш важливі характеристики випадкової величини - її математичне сподівання і дисперсію.
Математичне сподівання є середнє значення випадкової величини. Усереднення проводиться по великому числу випробувань. Для позначення таких середніх будемо використовувати кутові дужки
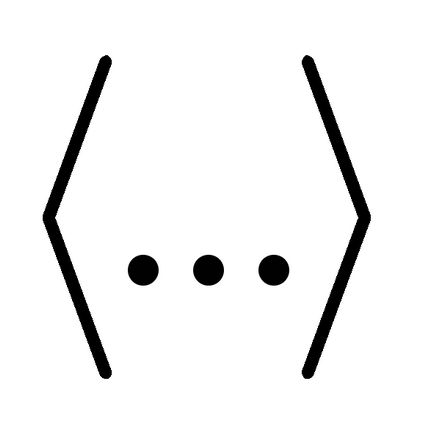
Середнє значення випадкової величини є сума добутків значень цієї величини на відповідне ймовірності:
або, якщо використовувати знак підсумовування,
Крім середнього значення, важливо також знати, наскільки сильно значення розглянутої величини відхиляються від її середнього значення або, інакше кажучи, наскільки широкий розкид значень випадкової величини.
Середнє значення відхилення від середнього (середнє значення різниці
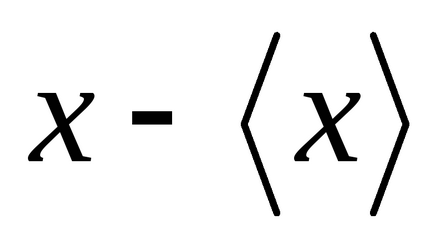
.
Тому розглядають середнє значення не найбільш відхилення від середнього, а квадрата відхилення, тобто:
Це і є дисперсія випадкової величини. яка позначається через
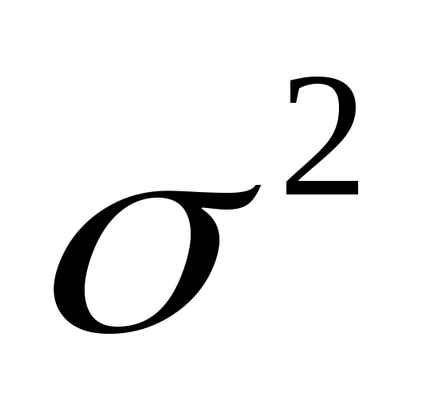
Квадратний корінь з дисперсії
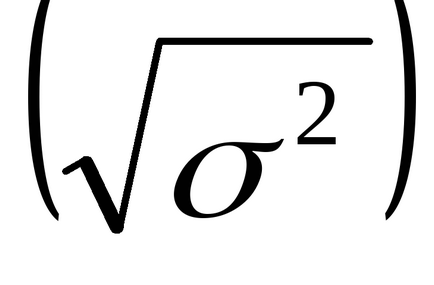
Отже, характеристики випадкової величини - математичне очікування і дисперсія - виражаються для дискретних величин через суми з розподілу ймовірностей (формули (2) - (4)).
Для безперервних випадкових величин замість сум використовують інтеграли, а замість розподілу ймовірностей розподіл щільності ймовірності:
де f (x) - щільність ймовірності випадкової величини.
Пояснимо, що мається на увазі під щільністю ймовірності. Нехай є набір з дуже великого числа N значень випадкової величини. Приклад - набір результатів N вимірювань деякої фізичної величини, при визначенні якої допускалися випадкові похибки. Приклад з молекулярної фізики - набір значень проекцій на будь-яку вісь швидкостей частинок газу. Нехай dN значень випадкової величини лежать в інтервалі від x до x + dx. Величина dN пропорційна ширині інтервалу dx і числу N. Законом (функцією) розподілу або щільністю ймовірності випадкової величини називається функція:
Щоб з'ясувати фізичний зміст функції розподілу, покладемо dx = 1, тобто розглянемо одиничний інтервал значень випадкової величини від x до x + 1. При цьому формула (7) спрощується і набуває вигляду:
Отже, функція розподілу показує, яка частка від загальної кількості значень випадкової величини лежить в одиничному інтервалі від x до x + 1.
Іншими словами, функція розподілу показує, наскільки ймовірним є те, що взяте навмання значення випадкової величини потрапить в одиничний інтервал від x до x + 1.
У багатьох випадках для опису випадкових величин справедливий так званий закон нормального розподілу (розподілу Гаусса). Цей розподіл має місце, якщо випадкова величина залежить від великої кількості факторів, що можуть вносити з однаковою ймовірністю позитивні і негативні відхилення. Прикладом може служити розподіл випадкових помилок при вимірюванні будь-якої фізичної величини або розподіл проекцій на координатну вісь швидкостей руху частинок газу. Можна показати, що закон нормального розподілу (закон Гаусса) має вигляд:
де х - довільне значення випадкової величини;
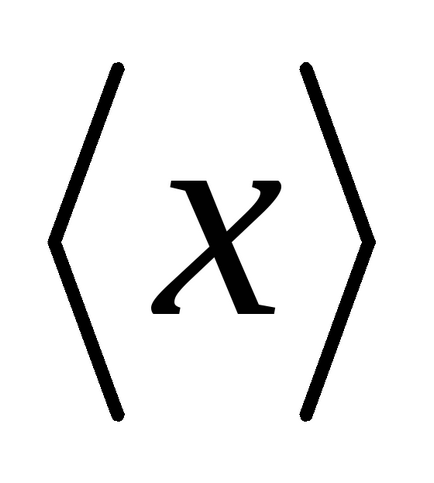
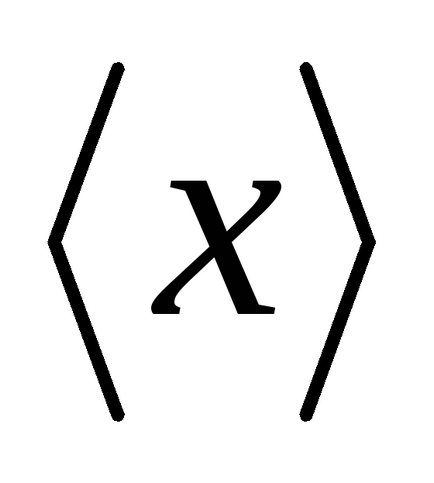
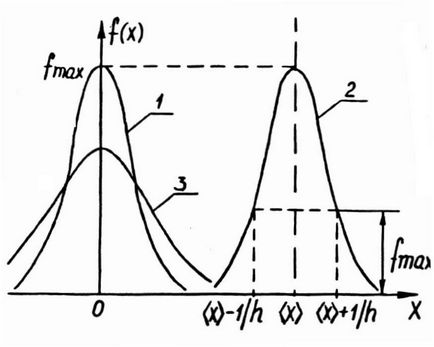
Малюнок 1 - Графік розподілу Гаусса.
1 -
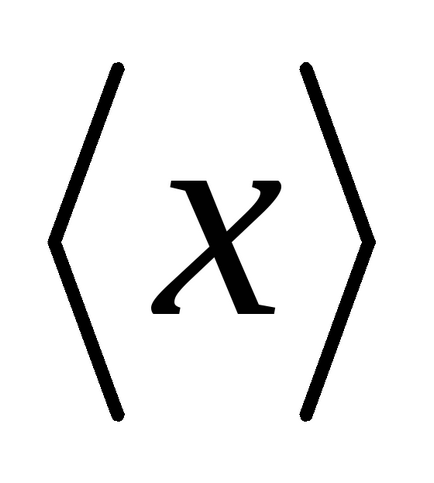
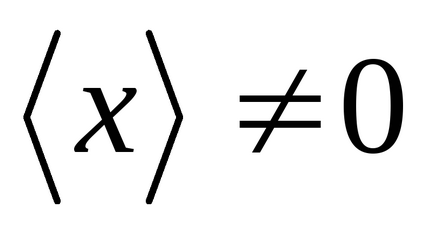
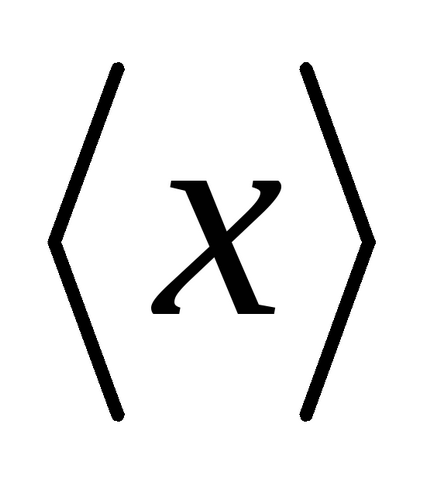
Нормальний розподіл характеризується також мірою точності
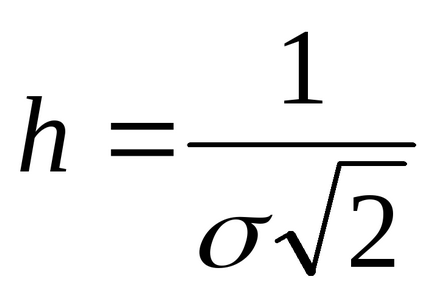
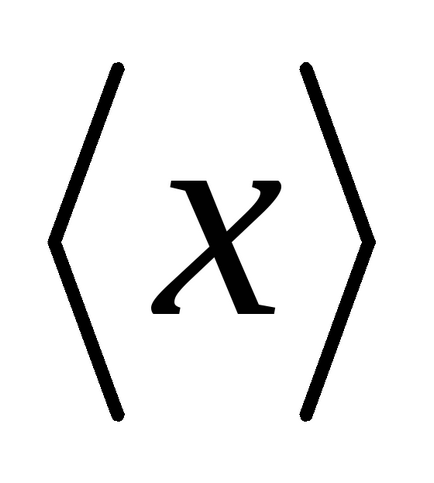
.
величина
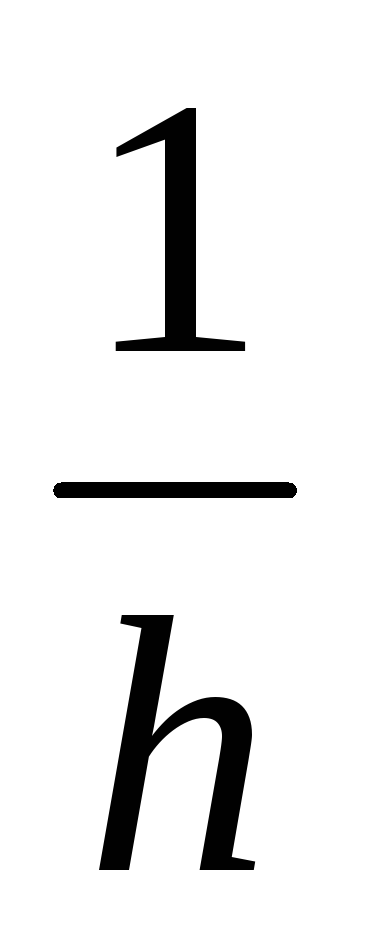
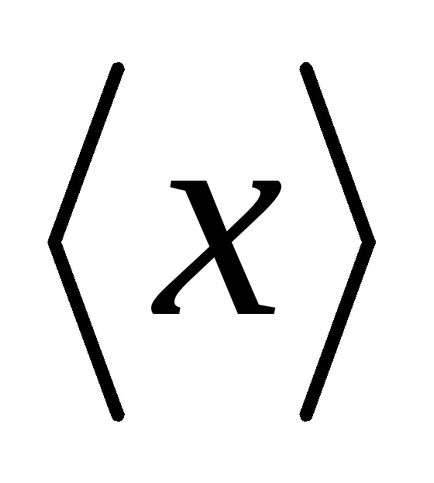
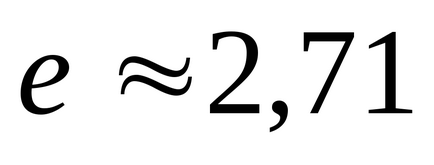
Отже, нормальним розподілом описується щільність ймовірності всіх безперервних випадкових величин, розкид значень яких обумовлений безліччю різноманітних факторів, що діють приблизно в однаковій мірі і незалежно один від одного. Максимум розподілу (рисунок 1) досягається при значенні х. рівному математичного сподівання
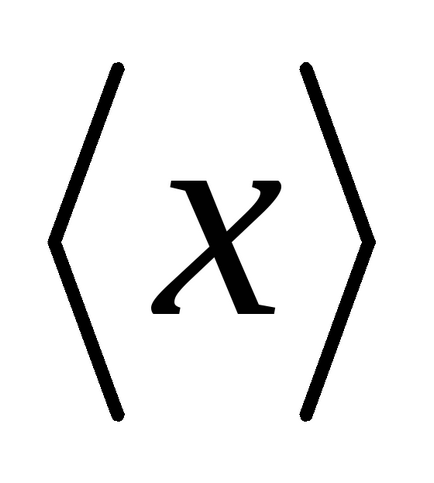
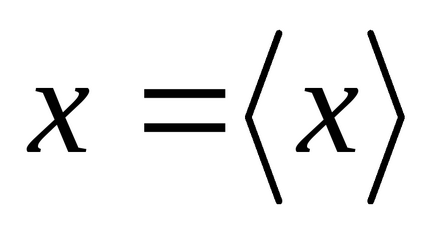
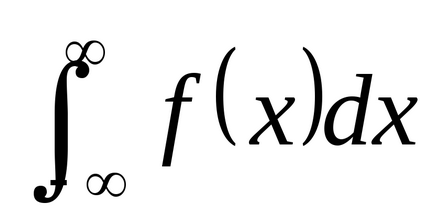
Розіб'ємо площа під кривою Гаусса (малюнок 2) вертикальними прямими на окремі ділянки. Спочатку розглянемо ділянку, відповідний проміжку.
Можна переконатися, що
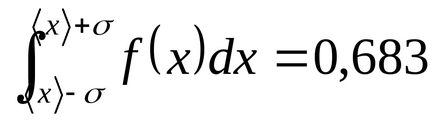
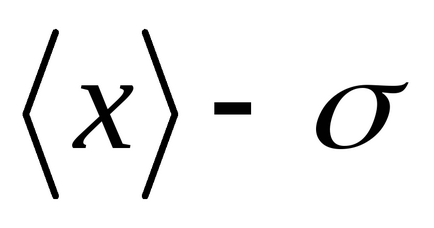
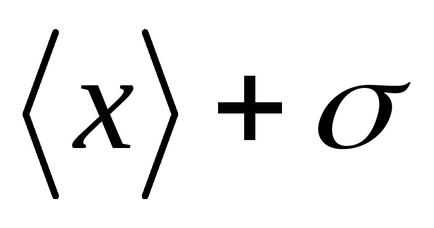
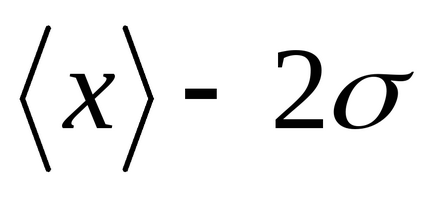
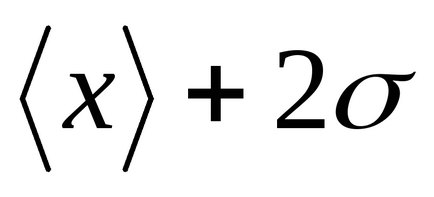
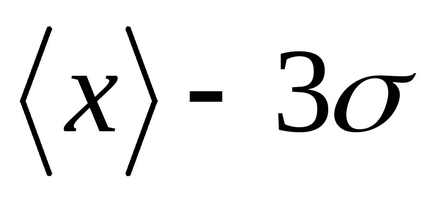
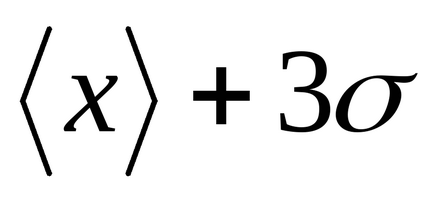
Т

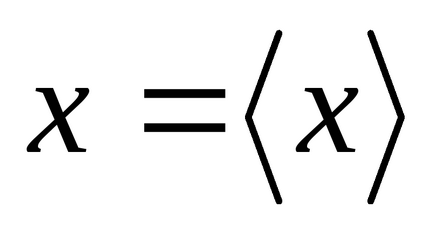
Рисунок2 - Правило «трьох сигм»
Як сказано вище, проекція vx швидкості частки газу на вісь х є випадкова величина з гауссовским законом розподілу, які приймають в даному випадку вид:
де m - маса частинки; k - постійна Больцмана; Т - абсолютна температура. З порівняння (9) і (10) випливає, що середнє значення проекції швидкості
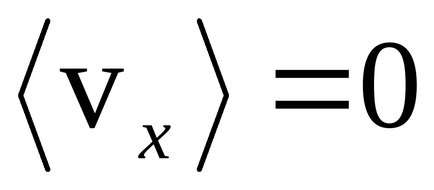
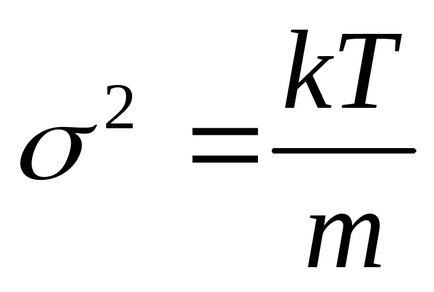
На відміну від проекції швидкості, яка отримує як негативні, так і позитивні значення, чисельне значення (модуль) швидкості частки не може бути негативним. Модуль швидкості частки газу - також випадкова величина, але вона описується не гауссовской, а так званої максвеллівською функцією розподілу частинок газу по скоростямF (v), пов'язаної з гауссовским розподілом проекцій швидкості формулою:
З графіка функції F (v) (рисунок 3) видно, що основна частка частинок газу має швидкості, близькі до так званої найбільш вірогідною швидкості vв. Частка частинок, що мають дуже маленьку (v → 0) або дуже велику швидкість (v → ∞), мала.
