Контрольна робота, соціальна мережа
Цільова функція споживання має вигляд. Ціна на перше благо дорівнює, а на друге благо. Дохід становить D = 550. Знайти:
а) криві байдужості;
б) оптимальний набір благ.
1) Криві байдужості мають вигляд:
Отримуємо безліч гіпербол розташованих в першій координатної чверті і розташованих на різній відстані від початку координат в залежності від значення константи С.
2) Знаходимо оптимальний набір благ. Завдання оптимального програмування має вигляд:
.
Для її вирішення висловлюємо з бюджетного обмеження одну змінну через іншу:.
Підставляємо в цільову функцію:.
Знаходимо похідну і прирівнюємо її до 0:
Таким чином, оптимальний набір благ становить 55/3 і 55/2 одиниць.
Є баланс двох взаємопов'язаних галузей (сільське господарство і машинобудування) за попередній рік.
Знайти кінцевий продукт кожної галузі, чисту продукцію кожної галузі, матрицю коефіцієнтів прямих витрат. Якою буде валовий продукт кожної галузі, якщо кінцевий продукт сільського господарства необхідно збільшити на 40%, а машинобудування зменшити на 20%. Матриця міжгалузевих матеріальних зв'язків xij і матриця валового випуску Xj наведені в таблиці.
, .
Кінцевий продукт визначимо за формулою:
,
де - одинична матриця, - матриця прямих витрат, елементи якої визначаються за правилом.
.
- кінцевий продукт галузей.
Знайдемо чисту продукцію галузей, використовуючи формулу:
.
Маємо - чиста продукція c / x,
- чиста продукція машинобудування.
Для знаходження валового продукту, відповідного новому кінцевого продукту виду, використовуємо формулу:
.
Знаходимо обернену матрицю:
.
Міжгалузевий баланс виробництва і розподілу продукції для 4 галузей має вигляд:
Знайти кінцевий продукт кожної галузі, чисту продукцію кожної галузі, матрицю коефіцієнтів прямих витрат. Якою буде кінцевий продукт кожної галузі, якщо валовий продукт першої галузі збільшиться в 2 рази, у другий збільшиться на половину, у третій не зміниться, у четвертій - зменшиться на 10 відсотків.
Матриця міжгалузевих матеріальних зв'язків xij і матриця валового випуску Xj наведені в таблиці:
1) Знайдемо чисту продукцію галузей, використовуючи формулу:
.
,
,
,
.
2) Кінцевий продукт галузей:
.
,
,
,
.
3) Елементи матриці прямих витрат визначаємо за правилом.
4) Новий валовий продукт.
Кінцевий продукт галузей:
.
,
,
,
.
З цієї виробничої функції знайти середні і граничні продуктивності кожного ресурсу, приватні еластичності випуску по кожному ресурсу, еластичність виробництва і граничну технологічну норму заміни.
, .
Граничні продуктивності рівні:
, .
Приватні еластичності рівні:
,.
Технологічна норма заміни є:.
Деякий підприємство витрачає а1 = 7 тис. Тонн ресурсу і b1 = 32 тис. Годин праці для випуску з1 = 65 тис. Одиниць продукції. В результаті розширення виробництва виявилося, що при витратах 2 = 8 тис. Тонн ресурсу випуск зріс до с2 = 67 тис. Одиниць продукції, а при збільшенні трудомісткості до b-2 = 34 тис. Годин, випуск зріс до с3 = 70 тис. Одиниць продукції. Знайти лінійну виробничу функцію і виробничу функцію Кобба-Дугласа.
Запишемо для зручності вихідні дані у вигляді таблиці:
Для знаходження b використовуємо перший стовпець таблиці:
В результаті лінійна виробнича функція має вигляд:
.
Виробнича функція Кобба-Дугласа має вигляд:
.
, .
Для знаходження b використовуємо перший стовпець таблиці:
В результаті виробнича функція Кобба-Дугласа має вигляд:
.
Виробниче об'єднання складається з 4 підприємств (n = 4). Загальна сума капітальних вкладень дорівнює 700 млн. Руб. (B = 700), що виділяються підприємством суми кратні 100 млн. Руб. Якщо j-е підприємство отримує інвестиції в обсязі x млн. Руб. то приріст річного прибутку на цьому підприємстві складе fj (x) млн. руб. на рік. Значення функцій fj (x) наведені в таблиці:
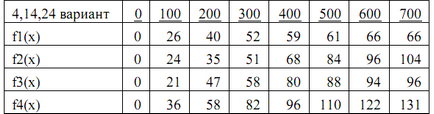
Потрібно знайти такий розподіл інвестицій між підприємствами, яке максимізує сумарний приріст прибутку на всіх підприємствах разом.
Складаємо першу допоміжну таблицю: