Інформаційні системи в методах оптимізації

Методичні вказівки
по виконанню практичних занять

Дисципліна - «Методи оптимізації»

Спеціальності - 230700.62 «Прикладна інформатика», 231000.62 «Програмна інженерія», 230400.62 «Інформаційні системи та технології», 080801 «Прикладна інформатика (в економіці)», 230105 «Програмне забезпечення обчислювальної техніки і автоматизованих систем», 230100.62 «Інформатика та обчислювальна техніка»

Допущено ФГБОУ ВПО «Держуніверситет-ННВК» для використання в навчальному процесі в якості методичних вказівок для вищої професійної освіти

Рецензент: к.т.н. доцент кафедри ІС О. В. Конюхова

Методичні вказівки містять опис п'яти практичних занять з дисципліни «Методи оптимізації». Вони присвячені виробленню у студентів навичок розробки математичних і інформаційних моделей процесів в предметної області; а також сприяють набуттю навичок експериментальних досліджень при виборі методу оптимізації, так само при вирішенні типових оптимізаційних задач. Методичні вказівки містять теоретичні відомості щодо запропонованих питань, практичні приклади та довідкову інформацію, необхідну для виконання лабораторних робіт.

Методичні вказівки призначені для студентів очної форми навчання спеціальностей 230700.62 «Прикладна інформатика», 231000.62 «Програмна інженерія», 230400.62 «Інформаційні системи та технології», 080801 «Прикладна інформатика (в економіці)», 230105 «Програмне забезпечення обчислювальної техніки і автоматизованих систем», 230100.62 «Інформатика та обчислювальна техніка».

Орловський державний технічний університет

Підписано до друку Формат 60 84 1 \ 16

Друк офсетний. Ум. печ. л.5,6. Тираж 10 прим.

Віддруковано з готового оригінал-макету

на поліграфічній базі ФГБОУ ВПО «Держуніверситет - ННВК»

1.Лінейное програмування: симплекс - метод 4

2.Спеціальние завдання лінійного програмування 19

3. Рішення цілочисельних задач 23

4. Рішення задач багатокритеріальної оптимізації 27

5. Мережева модель, розрахунок основних параметрів мережного графіка 31

Практичне заняття №1

Лінійне програмування: симплекс-метод рішення задач лінійного програмування, геометрична інтерпретація задач

Практичне заняття №2

Практичне заняття №3

Рішення задач по нелінійної оптимізації. Метод множників Лагранжа.

Практичне заняття №4

Мережева модель, розрахунок основних параметрів мережного графіка.

Побудова мережевого графіка

Мережеві графіки представляють собою орієнтовані графи, дуг або вершин яких приписані деякі числові значення.

Як правило, вершини, звані подіями, відповідають моментам часу початку або закінчення однієї або декількох операцій, а дуги - операціями.

Розрізняють три види подій: вихідне, завершальне і проміжне. Початкове - це така подія, з якого починається виконання комплексу операцій. Завершальне відповідає досягненню кінцевої мети, т. Е. Завершенню комплексу операцій. Мережеві графіки з кількома завершальними подіями називаються багатоцільовими. До проміжних відносяться всі інші події.

Події, як правило, позначаються кружками. Передбачається, що події не мають тривалості у часі.

Моментом здійснення події вважається момент закінчення виконання всіх вхідних в цю подію операцій. Поки не виконані всі вхідні в подія операції, не може здійснитися сама подія, і, відповідно, не може бути розпочато жодна з безпосередньо наступних за ним операцій.

Розрізняють три види операцій:

1) дійсна операція () - процес, що вимагає витрат часу і ресурсів (розробка проекту, підвезення матеріалів, виконання монтажних робіт і т. Д.);

2) операція - очікування () - процес, що вимагає тільки витрат часу (затвердіння бетону, природна сушка штукатурки перед початком малярних робіт, зростання рослин і т. Д.);

3) фіктивна операція (), або логічна залежність, відображає технологічну або ресурсну залежність у виконанні деяких операцій.

При побудові мережевих графіків необхідно дотримуватись певних правил:

1) в мережі не повинно бути подій (крім вихідного), в які не входить ні одна дуга;

2) не повинно бути подій (крім завершального), з яких не виходить жодної дуги;

3) мережа не повинна містити контурів;

4) будь-яка пара подій мережевого графіка може бути з'єднана не більше ніж однією дугою. Якщо зобразити одночасно виконуються три різні операції. . з загальними початковим і кінцевим подіями (Рис. 4.1), то виникає плутанина через те, що різні операції мають один і той же позначення (2,5). В цьому випадку рекомендується ввести додаткові події і з'єднати їх з подальшими фіктивними операціями (Рис. 4.2);

5) номер початкового події будь-якої операції повинен бути менше номера її кінцевого події.

Для відображення технологічної або ресурсної залежності у виконанні операцій застосовують фіктивні операції. Припустимо, що операція може виконуватися після завершення операцій і. а операція - лише після завершення операції.

Ця залежність представлена на Рис. 4.3, з якого видно, що операція слідує за операцією і фіктивної операцією (2, З).

Аналіз даних, наведених у цій таблиці, послідовності і взаємозалежності робіт, дозволяє побудувати мережевий графік представлений на рис. 4.4.

Інформаційні системи в методах оптимізації

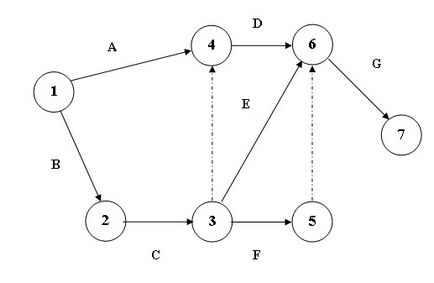
В даному мережевому графіку крім робіт, зазначених в таблиці, використані дві фіктивні роботи (3,4) і (5,6), позначені штриховими лініями. Ці роботи не вимагають часу на їх виконання і використовуються в графічному поданні проекту лише для того, щоб правильно відобразити взаємозв'язок між роботами.

Практичне заняття №5

Розділ математики, що вивчає конфліктні ситуації на основі їх математичних моделей, називається теорією ігор. Можна також сказати, що теорія ігор - математична теорія конфліктних ситуацій, що розробляє рекомендації по найбільш раціонального способу дій кожного з учасників в ході конфліктної ситуації, тобто таких дій, які забезпечували б йому найкращий результат.

Ігрові схеми можна застосовувати в багатьох економічних ситуаціях. Виграшем можуть при цьому виступати величина прибутку, собівартість, ефективність використання дефіцитних ресурсів, виробничих фондів, і т.д.

Істотним обставиною є те, що методи і рекомендації теорії ігор розроблені стосовно до таких конфліктних ситуацій, які мають властивість багаторазової повторюваності. Якщо конфліктна ситуація реалізується одноразово або обмежене число раз, то рекомендації теорії ігор стають малоефективними.

Аналіз реальної конфліктної ситуації вимагає її істотного (іноді радикального) спрощення - обліку лише найбільш істотних для конфлікту факторів. У зв'язку з цим, можна розглядати гру як спрощену математичну модель конфліктної ситуації, що характеризується наявністю певних правил. Ці правила встановлюють:

1. вибір способу дії гравців на кожному етапі гри;

2. інформацію, якою володіє кожен гравець при здійсненні таких виборів;

3. плату для кожного гравця після завершення будь-якого етапу гри.

Стратегією гри називається сукупність правил, що визначають поведінку гравця протягом всієї гри. Стратегії кожного гравця визначають результати або платежі в грі; при цьому кожен гравець має деякий безліч (кінцеве або нескінченне) можливих стратегій.

До числа визначальних характеристик ігор можна віднести наступні:

1. є конфліктуючих сторін (гравців), які приймають рішення, інтереси яких не збігаються;

2. сформульовані правила вибору допустимих стратегій, відомі гравцям;

3. визначено набір можливих кінцевих станів гри (наприклад, виграш, програш, нічия);

4. всім учасникам гри (гравцям) заздалегідь відомі платежі, відповідні кожному можливому кінцевого стану.

Конфліктні ситуації, що зустрічаються в практиці, породжують різні види ігор. Класифікація ігор можлива за різними ознаками.

А) За кількістю гравців. У грі може брати участь будь-яке кінцеве число гравців. Якщо гравців всього двоє, або гравці об'єднуються в дві групи, що переслідують протилежні цілі, то має місце парна гра. Залежно від кількості стратегій в грі вони діляться на кінцеві і нескінченні.

Б) Залежно від взаємовідносин учасників розрізняють беськоаліционниє (учасники не мають права укладати угоди) і коаліційні ігри (іноді використовуються синоніми - некооперативного і кооперативні ігри відповідно).

В) За характером виграшів ігри поділяються на ігри з нульовою сумою і ненульовий сумою. В іграх з нульовою сумою загальний капітал гравців не змінюється, а лише перерозподіляється в ході гри, в зв'язку з чим сума виграшів дорівнює нулю (при цьому програш розглядається як негативний виграш). В іграх з ненульовою сумою сума виграшів відмінна від нуля.

Г) По виду функції виграшу ігри поділяються на матричні, біматричних і ін. В матричних іграх (за двох учасників) виграші першого гравця задаються матрицею, в біматричних - виграші кожного гравця задаються своєї матрицею.

Д) За кількістю ходів гри діляться на одноходові (виграш розподіляється після одного ходу кожного гравця) і багатоходові (виграш розподіляється після декількох ходів).

Стратегія гравця називається оптимальною, якщо вона забезпечує даному гравцю при багаторазовому повторенні гри максимально можливий середній виграш або мінімально можливий середній програш, незалежно від поведінки противника.

Надалі ми обмежимося розглядом парних матричних ігор з нульовою сумою. Завдання стратегій двох гравців в парній грі такого типу повністю визначає її результат, тобто виграш одного або програш іншого. Як уже зазначалося, результати кінцевої парної гри з нульовою сумою можна задавати матрицею, рядки і стовпці якої відповідають різним стратегіям 1-го і 2-го гравців відповідно, а її елементи - виграшами одного боку (рівні програшів інший). Ця матриця називається платіжною матрицею або матрицею гри.

Ігри без сідлових точок

Отже, якщо матриця гри містить седловую точку, то її рішення знаходиться за принципом минимакса. Розглянемо методику рішення гри, в платіжної матриці якої відсутній сідлова точка. Застосування мінімаксний стратегій кожним з гравців забезпечує першому виграш не менше. а другого програш не більш. Враховуючи що . природно для гравця I бажання збільшити виграш, а для гравця II - зменшити програш. Пошук такого рішення призводить до застосування складної стратегії, що складається у випадковому застосуванні двох і більше чистих стратегій з певними можливостями. Така складна стратегія в теорії ігор називається змішаною. Змішані стратегії гравців I і II будемо позначати, відповідно,

де. # 8209; ймовірності застосування відповідних чистих стратегій. Очевидно, повинні виконуватися умови нормування для вірогідності

Одна з основних теорем теорії ігор стверджує, що будь-яка кінцева гра двох осіб з нульовою сумою має, принаймні, одне рішення, можливо, в змішаних стратегіях. З цієї теореми випливає, що кожна кінцева гра має ціну. Позначимо її так само, як чисту ціну гри, через. Ціна гри - середній виграш, який припадає на одну партію, - завжди задовольняє умові. тобто лежить між нижньої () і верхньої () цінами гри. Отже, кожен гравець при багаторазовому повторенні гри, дотримуючись змішаних стратегій, отримує більш вигідний для себе результат. Оптимальне рішення гри в змішаних стратегіях, так само як і рішення в чистих стратегіях, характеризується тим, що кожен з гравців не зацікавлений у відході від своєї оптимальної змішаної стратегії, якщо його противник застосовує оптимальну змішану стратегію, так як це йому невигідно.

Стратегії гравців, що входять до їх оптимальні змішані стратегії, називаються активними.

5.5 Використання лінійної оптимізації при вирішенні матричних ігор

Нехай гра не має оптимального рішення в чистих стратегіях, тобто сідлова точка відсутня.

Будемо вважати, що всі елементи платіжної матриці невід'ємні (якщо це не так, то можна до всіх елементів матриці додати деяке число L, що переводить платежі в область невід'ємних значень - очевидно, при цьому ціна гри збільшиться на L, а рішення задачі не зміниться). Таким чином, припускаємо, що> 0.

Будемо шукати рішення гри в змішаних стратегіях

Застосування гравцем I оптимальної змішаної стратегії гарантує йому, незалежно від поведінки гравця II, виграш, не менший ціни гри.

Нехай гравець II застосовує свою активну чисту j-ю стратегію, а гравець I - свою оптимальну стратегію. Тоді середній виграш гравця I буде дорівнює

З огляду на, що не може бути менше. запишемо умови:

Розділивши ліву і праву частини кожного з нерівностей (5.4) на ціну гри. отримаємо

При використанні позначень

нерівності (5.5) приймуть вид

де, очевидно, все. так як .

і в силу визначення (5.6) випливає, що змінні () задовольняють умові

З огляду на, що гравець I прагне максимізувати. отримуємо лінійну функцію

Таким чином, завдання вирішення гри звелася до наступної задачі лінійної оптимізації: знайти невід'ємні значення змінних мінімізують лінійну функцію (5.8) і задовольняють обмеженням (5.7).

З рішення задачі лінійної оптимізації легко знайти ціну гри та оптимальну стратегію гравця I:

У свою чергу, оптимальна стратегія гравця II

може бути знайдена з виразу

де - невід'ємні змінні завдання лінійної оптимізації

яка є двоїстої по відношенню до задачі, представленої умовами (5.7) і (5.8).

У цій системі нерівностей змінні

Таким чином, оптимальні стратегії

гри з платіжною матрицею () можуть бути знайдені шляхом рішення симетричною пари двоїстих задач лінійної оптимізації.

Вихідна задача Двоїста задача

Ціна гри і ймовірності застосування стратегій гравцями I і II рівні

5.6 Завдання для самостійного рішення

Шляхом зведення двоїстих задач лінійного програмування знайти оптимальні змішані стратегії і ціну гри матричних ігор з такими платіжними матрицями: