хвильова оптика
1.1.5. Протяжні джерела світла
У попередніх розділах ми обговорювали вплив немонохроматичності джерела світла на характер спостережуваного інтерференційної картини. Весь коло виникаючих при цьому питань прийнято об'єднувати загальним терміном «тимчасова когерентність». Існує й інший, не менш важливий, коло питань, що виникають при використанні в інтерференційних дослідах протяжних джерел. Ці питання об'єднуються терміном «просторова когерентність».
Протяжний джерело світла можна розглядати як сукупність точкових некогерентних джерел. Інтерференцію можуть створювати тільки хвилі, що прийшли в точку спостереження за двома різними шляхами інтерференційної схеми від одного і того ж елементарного джерела. Тому картини, отримані від різних точок протяжного джерела, потрібно складати по інтенсивності. Якщо взяти до уваги, що ці картини в площині спостереження зрушені відносно один одного, то стає ясно, чому виникає розмиття інтерференційних смуг в разі протяжного джерела.
Розглянемо як приклад схему досвіду Юнга (рис. 1.10).
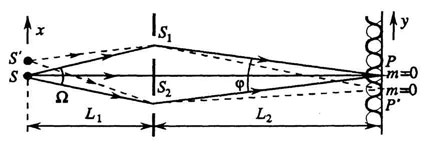
Зсув інтерференційних смуг в досвіді Юнга.
Якщо точкове джерело S знаходиться на осі системи, то різниця ходу звертається в нуль в точці спостереження P. також знаходиться на осі. Тут розташовується інтерференційний максимум нульового порядку (нульова интерференционная смуга). Для точкового джерела S ', розташованого на відстані x від осі, нульова смуга (а, отже, і вся інтерференційна картина) зміститься на деяку відстань
Складаючи по інтенсивності ці дві зсунуті інтерференційні картини (мають один і той же просторовий масштаб), ми отримаємо сумарну картину, видность якої істотно залежить від відстані x між джерелами S і S ', геометричних параметрів схеми і довжини хвилі. Зокрема, якщо інтерференційні смуги від S 'змістилися на півшпальти, то видность картинки звертається в нуль (при рівній інтенсивності джерел). Цей випадок зображений на рис. 1.10.
Нехай тепер джерелом світла є рівномірно світиться смужка ширини b. Вважаючи, що, (d - відстань між щілинами і), і виконавши інтегрування по x в межах, можна отримати такий вираз для розподілу інтенсивності в сумарною інтерференційної картини