глава друга
16.Цепь з 28 кісток.
Чому 28 кісток доміно можна викласти з дотриманням правил гри в одну безперервну ланцюг?
17.Начало і кінець ланцюга.
Коли 28 кісток доміно викладені в ланцюг, на одному її кінці виявилося 5 очок.
Скільки очок на іншому кінці?
18.Фокус з доміно.
Ваш товариш бере одну з кісток доміно і пропонує вам з інших 27 скласти безперервний ланцюг, стверджуючи, що це завжди можливо, яка б кістка не була взята. Сам же він видаляється в сусідню кімнату, щоб не бачити вашої ланцюга.
Ви приступаєте до роботи і переконуєтесь, що товариш ваш прав: 27 кісток виклалися в один ланцюг. Ще більш дивно те, що товариш, залишаючись в сусідній кімнаті і не бачачи вашої ланцюга, оголошує звідти, які числа очок на її кінцях.
Як може він це знати? І чому він упевнений, що з будь-яких 27 кісток доміно складеться безперервний ланцюг?
Мал. 5 зображує квадратну рамку, викладену з кісток доміно з дотриманням правил гри. Сторони рамки рівні по довжині, але не однакові за сумою очок: верхній і лівий ряди укладають по 44 очка, інші ж два ряди - 59 і 32.
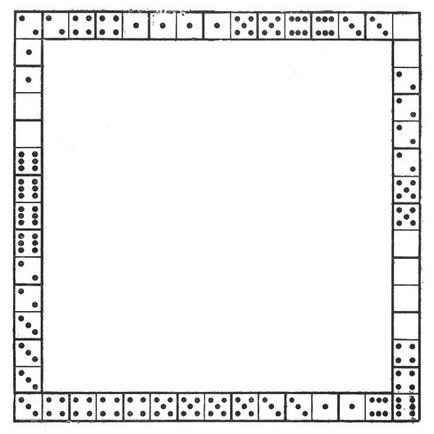
Мал. 5. Квадратна рамка
Чи можете ви викласти таку квадратну рамку, всі сторони якої укладали б однакову суму очок - саме 44?
20.Семь квадратів.
Чотири кістки доміно можна вибрати так, щоб з них склався квадратик з рівною сумою очок на кожній стороні. (Приклад ви бачите на рис. 6: склавши окуляри на кожній стороні квадратика, у всіх випадках отримаєте 11.)
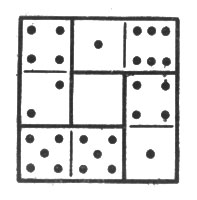
Мал. 6. Склавши окуляри на кожній стороні квадратика, у всіх випадках отримаєте 11
Чи можете ви з повного набору доміно скласти одночасно сім таких квадратів? Не потрібно, щоб сума очок на одній стороні була у всіх квадратів одна і та ж; треба лише, щоб кожен квадрат мав на своїх чотирьох сторонах однакову суму очок.
21.Магіческіе квадрати з доміно.
На рис. 7 показаний квадрат з 18 кісточок доміно, чудовий тим, що сума очок будь-якого його ряду - поздовжнього, поперечного або діагонального - одна і та ж: 13. Подібні квадрати здавна називаються "магічними".

Мал. 7. Квадрат з 18 кісточок доміно, чудовий тим, що сума очок будь-якого його ряду - поздовжнього, поперечного або діагонального - одна і та ж: 13
Вам пропонується скласти кілька таких же 18-кісточкових магічних квадратів, але з іншого сумою очок в ряду. 13 - найменша сума в рядах магічного квадрата, складеного з 18 кісток. Найбільша сума - 23.
22.Прогрессія з доміно.
Ви бачите на рис. 8 шість кісточок доміно, викладених за правилами гри і відрізняються тим, що число очок на кісточках (на двох половинах кожної кісточки) зростає на 1. Ряд починається з 4 і складається з наступних чисел очок:
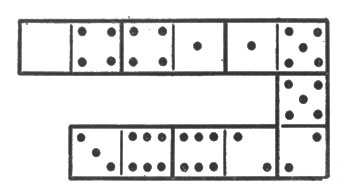
Мал. 8. Шість кісточок доміно, викладених за правилами гри і відрізняються тим, що число очок на кісточках (на двох половинах кожної кісточки) зростає на 1
Такий ряд чисел, які зростають (або зменшуються) на одну і ту ж величину, називається "арифметичною прогресією". У нашому ряду кожне число більше попереднього на 1; але в прогресії може бути і будь-яка інша "різниця".
Завдання полягає в тому, щоб скласти ще кілька 6-кісточкових прогресій.