Гіпербола, все про гіперболи
визначення гіперболи
Гіперболою називається геометричне місце точок площини, для якої абсолютна величина різниці відстаней до двох фіксованих точок і цій площині, званих фокусами, є величина постійна.
Фокуси і гіперболи природно вважати різними, тому що якщо зазначена у визначенні постійна не дорівнює нулю, то немає жодної точки площині при збігу і, яка б задовольняла вимогам визначення гіперболи. Якщо ж ця постійна дорівнює нулю і збігається з, то будь-яка точка площині задовольняє вимогам визначення гіперболи.
Канонічне рівняння гіперболи
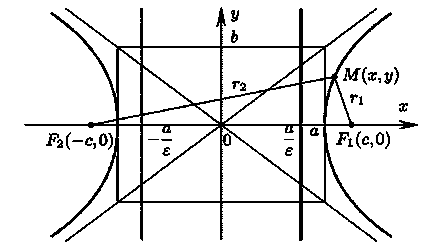
де. Дійсна піввісь гіперболи дорівнює, а уявна піввісь дорівнює.
Вершинами гіперболи називаються точки.
Фокуси гіперболи мають координати і, де.
Ексцентриситетом гіперболи називається величина, що дорівнює
Для гіперболи величина.
Директриси гіперболи задаються рівняннями
Асимптотами гіперболи є прямі.
Гіпербола називається сполученої до гіперболи, вона має ті ж асимптоти, але її гілки розташовані в іншій парі вертикальних кутів між асимптотами.