Геометричні застосування криволінійних інтегралів
Площа області, обмеженій замкненій кривій;
Обсяг тіла, утвореного обертанням замкнутої кривої щодо деякої осі.
Нехай \ (C \) є гладкою, кусочно-безперервною кривою, яка описується вектором \ (\ mathbf \ left (t \ right), \, \ alpha \ le t \ le \ beta. \) Довжина даної кривої виражається наступним криволінійним інтегралом \ [> = >>> \ left (t \ right)> \ right | dt >> = >>> \ right)> ^ 2> + >>> \ right)> ^ 2> + >>> \ right) > ^ 2 >> dt>,> \] де \ (\ large \ frac >>> \ normalsize \) - похідна, а \ (x \ left (t \ right), y \ left (t \ right), z \ left (t \ right) \) - компоненти векторної функції \ (\ mathbf \ left (t \ right). \)
Якщо крива \ (C \) задана в площині, то її довжина виражається формулою \ [> = >>> \ left (t \ right)> \ right | dt >> = >>> \ right)> ^ 2> +> >> \ right)> ^ 2 >> dt>.> \] Якщо крива \ (C \) являє собою графік явно заданої, безперервної і диференціюється \ (y = f \ left (x \ right) \) в площині \ (Oxy, \) то довжина такої кривої обчислюється за формулою \ [L = \ int \ limits_a ^ b >>> \ right)> ^ 2 >> dx>. \] Нарешті, якщо крива \ (C \) задана в полярних координатах рівнянням \ (r = r \ left (\ theta \ right), \, \ alpha \ le \ theta \ le \ beta, \) і функція \ (r \ left (\ theta \ right) \) є безперервною і диференціюється в інтервалі \ (\ left [\ right], \) то довжина кривої визначається виразом \ [L = \ int \ limits_ \ alpha ^ \ beta >>> \ right)> ^ 2> +> d \ theta>. \]
Площа області, обмеженій замкненій кривій
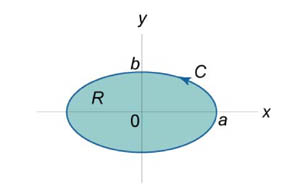
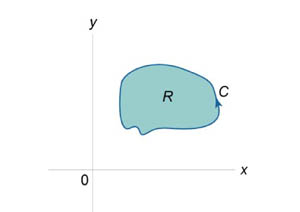
Нехай \ (C \) є гладкою, кусочно-безперервною і замкнутої кривої, заданої в площині \ (Oxy \) (рисунок \ (1 \)). Тоді площа області \ (R, \) обмеженою даної кривої, визначається формулами \ [= - \ oint \ limits_C> = \ int \ limits_C.> \] Тут мається на увазі, що обхід кривої \ (C \) проводиться проти годинникової стрілки.
Обсяг тіла, утвореного обертанням замкнутої кривої щодо осі Ox
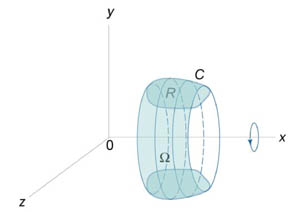
Припустимо, що область \ (R \) розташована у верхній півплощині \ (y \ ge 0 \) і обмежена гладкою, кусочно-безперервною і замкнутої кривої \ (C, \) обхід якої здійснюється проти годинникової стрілки. В результаті обертання області \ (R \) навколо осі \ (Ox \) утворюється тіло \ (\ Omega \) (рисунок \ (2 \)). Обсяг даного тіла визначається формулами \ [dx >> = <- 2\pi \oint\limits_C> = <- \frac\oint\limits_C dx> .> \]
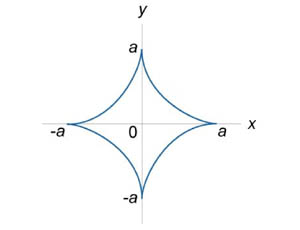
Знайти довжину кривої \ (a = \) за умови \ (0 \ le x \ le 5a, \, y \ ge 0. \)
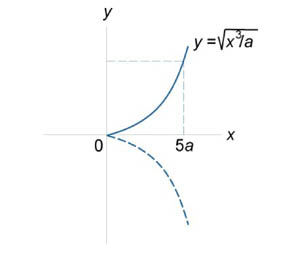
Знайти довжину просторової кривої, заданої параметрично у вигляді \ (\ mathbf \ left (t \ right) = \ left (, 2> \ right), \) де \ (0 \ le t \ le 1. \)
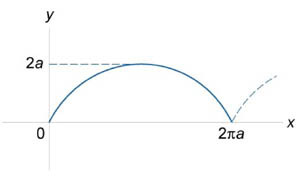
Знайти довжину циклоїди, заданої в параметричному вигляді вектором \ (\ mathbf \ left (t \ right) = \ left (\ right), a \ left (\ right)> \ right) \) в інтервалі \ (0 \ le t \ le 2 \ pi \) (рисунок \ (5 \)).
Знайти площу області, обмеженої гіперболою \ (y = \ large \ frac \ normalsize, \) віссю \ (Ox \) і вертикальними прямими \ (x = 1, \) \ (x = 2 \) (рисунок \ (7 \) ).
Обчислимо площу за допомогою криволінійного інтеграла. \ [> = <- \int\limits_ - \int\limits_ - \int\limits_ - \int\limits_ .> \] Знайдемо окремо кожен з інтегралів. \ [- \ int \ limits_ = - \ int \ limits_1 ^ 2 = 0, \] \ [- \ int \ limits_ = - \ int \ limits_0 ^ 0 = 0, \] \ [= - \ int \ limits_2 ^ 1 >>> = \ right)> \ right | _2 ^ 1> = <- \ln 1 + \ln 2 = \ln 2,> \] \ [- \ int \ limits_ = - \ int \ limits_0 ^ 0 = 0. \] Отже, площа заданої області дорівнює \ [S = \ ln 2. \]
Знайти площу області, обмеженої еліпсом, заданим параметрически у вигляді \ (x = a \ cos t, \; y = b \ sin t, \; 0 \ le t \ le 2 \ pi \) (рисунок \ (8 \)) .