Формула сили натягу нитки в фізиці
Визначення і формула сили натягу нитки
Силу натягу визначають як рівнодіюча сил, прикладених до нитки, рівну їй по модулю, але протилежно спрямовану. Усталеного символу (букви), що позначає силу натягу немає. Її позначають і просто і, і. Математично визначення для сили натягу нитки можна записати як:
де = векторна сума всіх сил, які діють на нитку. Сила натягу нитки завжди спрямована по нитці (або підвісу).
Найчастіше в задачах і прикладах розглядають нитка, масою якої можна знехтувати. Її називають невагомою.
Ще одним важливим характеристикою нитки при розрахунку сили натягу є її розтяжність. Якщо досліджується невагома і нерозтяжна нитку, то така нитка вважається просто проводить через себе силу. У тому випадку, коли необхідно враховувати розтягнення нитки, застосовують закон Гука, при цьому:
де k - коефіцієнт жорсткості нитки, - подовження нитки при розтягуванні.
Одиниці виміру сили натягу нитки
Основною одиницею виміру сили натягу нитки (як і будь-якої сили) в системі СІ є: [T] = Н
Приклади розв'язання задач
Завдання. Невагома, нерозтяжна нитка витримує силу натягу T = 4400Н. З яким максимальним прискоренням можна піднімати вантаж масою m = 400 кг, який підвішують на цю нитку, щоб вона не розірвалася?
Рішення. Зобразимо на рис.1 всі сили, що діють на вантаж, і запишемо другий закон Ньютона. Тіло будемо вважати матеріальною точкою, всі сили доданими до центру мас тіла.
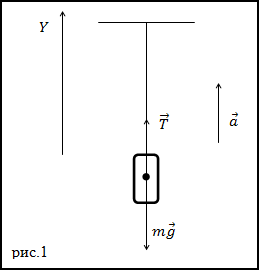
де - сила натягу нитки. Запишемо проекцію рівняння (1.1) на вісь Y:
З виразу (1.2) отримаємо прискорення:
Всі дані в завданні представлені в одиницях системи СІ, проведемо обчислення:
Завдання. Шарик, який має масу m = 0,1 кг прикріплений до нитки (рис.2) рухається по колу, розташованої в горизонтальній площині. Знайдіть модуль сили натягу нитки, якщо довжина нитки l = 5 м, радіус кола R = 3м.
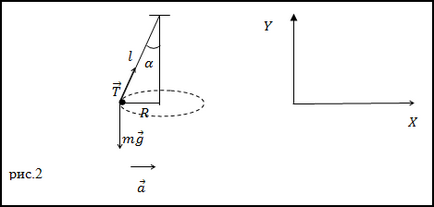
Рішення. Запишемо другий закон Ньютона для сил, прикладених до кульки, що обертається по колу з доцентровим прискоренням:
Знайдемо проекції даного рівняння на зазначені на рис.2 осі X і Y:
З рівняння (2.3) отримаємо формулу для модуля сили натягу нитки:
З рис.2 видно, що:
Підставами (2.5) замість в вираз (2.4), отримаємо:
Так як всі дані в умовах завдання наведені в одиницях системи СІ, проведемо обчислення: