Фіз-мат клас 1
Якщо - попарно перпендикулярні поодинокі вектори, так званий ортонормованій базис. то будь-який вектор простору може бути єдиним чином розкладений по цим векторах, тобто представлений у вигляді
.
Числа називаються декартовими координатами вектора в базисі. Декартові координати вектора є проекціями цього вектора на відповідні осі системи координат:
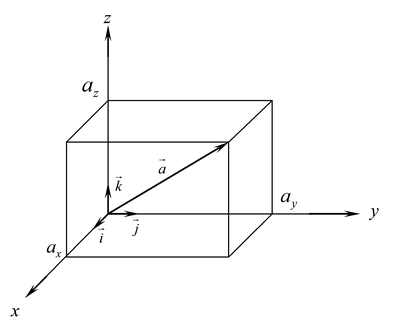
Якщо числа відмінні від нуля, то можна зобразити за допомогою діагоналі прямокутного паралелепіпеда, у якого довжини ребер рівні
Якщо вектор відкладений від точки з координатами і закінчуються в точці з координатами, то координати вектора визначаються через координати початку і кінця вектора за формулами:
Якщо і - два довільних вектора, то:
Координати суми векторів дорівнюють сумі відповідних координат доданків.
Координати різниці векторів рівні різниці відповідних координат цих векторів
Координати твори на число дорівнюють добутку відповідних координат векторів на дане число
Лінійна комбінація векторів і, де і - довільні числа, відповідають координати
Скалярний добуток векторів визначається як
Величина скалярного твори визначається через координати векторів за формулою
Довжина вектора з координатами дається формулою
Кут між векторами і визначається з рівності
Будь-яке лінійне рівняння
зв'язують координати визначає безліч точок простору, що лежать на площині, і, навпаки, кожну площину можна задати лінійним рівнянням з трьома невідомими, що мають принаймні один ненульовий коефіцієнт при змінних.
Кут між двома площинами і знаходиться як кут між перпендикулярними векторами і, тобто за формулою
Відстань від точки до площини дається формулою