Евристичне програмування, aideus
До моменту появи комп'ютерів розрізнені дані психології, етнології, зоопсихології, педагогіки і методології науки свідчили про те, що інтелект зручно представляти як здатність до вирішення завдань (проблемних ситуацій), а сам процес рішення (мислення) реалізується як пошук такого ланцюжка дій, яка початкову ситуацію (умова завдання) переводила б в кінцеву ситуацію (відповідь). Починаючи з деякого рівня розвитку живих організмів, перебір дій шляхом їх фактичного виконання замінюється «віртуальним» перебором «згорнутих» дій. В математиці в цей час з метою суворого опису правильних міркувань було формалізовано поняття алгоритму, що розгортається в залежну від вихідних даних послідовність дій і описує рішення задачі в загальному вигляді. Комп'ютери були створені як пристрої, автоматично виконують алгоритми, т. Е. Які вирішують завдання, представлені в символьній формі. Однак залишався ключове питання: як знаходити самі алгоритми або хоча б лінійні ланцюжка послідовних дій? Через NP-повноти або навіть нерозв'язності загальної проблеми пошуку повний перебір всіх можливих варіантів у багатьох випадках виявляється неможливим.
Згідно Пойя, людині вдається в якійсь мірі долати цю проблему, використовуючи евристики - прийоми, що полегшують рішення завдань. Але чи можна евристики запрограмувати? А якщо можна, в якому вигляді це слід робити? Спроба вчених відповісти на ці питання привела в 1950-60-х роках до виникнення однієї з перших парадигм штучного інтелекту, що отримала назву «евристичне програмування». В області ІІ з моменту її виникнення існувало багато різних напрямків досліджень, але саме евристичне програмування можна охарактеризувати як першу спробу створення дійсно загальної теорії штучного інтелекту.
В евристичному програмуванні проблема штучного інтелекту часто вивчалася на прикладі інтелектуальних ігор, таких як шашки, шахи і т. Д. З одного боку, «всесвіт» будь-настільної гри задається маленьким набором дуже простих законів, які легко запрограмувати. З іншого боку, в процесі гри, наприклад в шахи, безумовно, необхідно думати. Завдання докази математичних теорем і завдання планування також широко досліджувалися в евристичному програмуванні, проте вони вимагали додаткових предметних знань (наприклад, пояснити людині правила гри в шахи набагато простіше, ніж правила інтегрування) і були менш показовими і більш складними в реалізації. Спробуємо спочатку подивитися на проблему мислення на прикладі простої гри.
Наступний розгляд можуть здатися тривіальними в силу того, що добре відомі і більш складні методи. Однак уявіть себе на місці першовідкривачів, яким абсолютно нічого ще не було відомо і нізвідки було запозичити готові рішення. Це допоможе краще зрозуміти причини і шляхи розвитку області евристичного програмування і досліджень штучного інтелекту взагалі. Адже серед звичних готових рішень багато що може бути випадковим і не оптимальним, в зв'язку з чим непогано переглядати старі результати в більш широкому контексті сучасних уявлень.
Нехай перед нами стоїть завдання навчити комп'ютер грати в найпростішу інтелектуальну гру - «хрестики-нулики» на поле 3 × 3. Як би ви стали вирішувати таке завдання?
Перше бажання полягає в тому, щоб в явному вигляді вказати, які ходи повинен робити комп'ютер. І новачки зазвичай йдуть саме цим шляхом, оскільки він здається найпростішим і контрольованим. Нехай комп'ютер грає хрестиками. Тоді можна явно задати, що перший хід робиться в центр поля. Далі, однак, відповідь комп'ютера повинен залежати від ходу гравця.
Позначимо клітини дошки в «шаховому» стилі: від A1 до C3. Тоді такий алгоритм гри (з використанням синтаксису мови С ++) може виглядати приблизно так
Такий алгоритм схожий на системі найпростіших рефлексів. Однак звідки беруться ходи, записані в нашій програмі? Щоб переконатися в тому, що деякий наш хід призводить до виграшу, потрібно перевірити всі можливі ходи супротивника. Це можна представити у вигляді дерева гри, також званого деревом варіантів для неігрових завдань. На наступному малюнку показаний приклад фрагмента дерева гри для «хрестиків-нуликів» на поле 3 × 3. Корінь цього дерева є порожню дошку, а виходять з нього гілки відповідають можливим ходам першого гравця. Ці гілки ведуть в нові стани ігрового світу, з кожного з яких також виходять гілки, відповідні дозволеним ходам другого гравця, і так далі. У разі неігрових завдань в корені дерева варіантів може перебувати, наприклад, вона вирішується рівняння, а гілки будуть відповідати допустимим операціями з перетворення цього виразу.
По суті, таке дерево описує простір станів - сукупність станів, в яких може перебувати деякий, наприклад ігровий, світ із зазначенням можливих переходів між станами. Для деяких завдань це простір може здаватися шляхом явного перерахування всіх можливих станів і переходів між ними, але частіше воно задається неявно - у формі правил (гри, інтегрування і т. Д.). На основі правил може бути організована породжує процедура, явно будує дерево варіантів.
Ми користуємося цією процедурою, щоб побудувати дерево гри і знайти на ньому такі відповіді, які б приводили
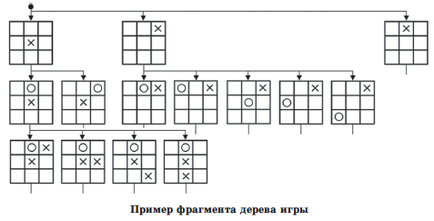
до перемоги або, якщо це неможливо, до нічиєї. Їх ми і заносимо в нашу програму. А чи не можна, щоб комп'ютерна програма, яка грає в «хрестики-нулики», сама будувала дерево варіантів на основі відомої породжує процедури? Природно, більш елегантний (чим представлений вище) алгоритм і мав би сам будувати дерево гри і вибирати найкращий хід, як це робимо ми.
Здійснити таке побудова без зберігання в пам'яті додаткової копії ігрового поля (а в більш загальному випадку - моделі світу) проблематично. Нехай field [3] [3] - допоміжний масив 3 × 3, значення в осередку якого встановлено в '-', якщо відповідна клітка не зайнята, і в 'X' і 'O', якщо там «хрестик» і «нулик» відповідно. Тоді породжує процедура може бути записана в такій формі:
Якщо попередньо встановити всі значення масиву field як порожні ( '-'), а потім запустити цю процедуру tree_ search ( 'X'), то в процесі її роботи в масиві field черзі виявляться всі можливі комбінації розташування хрестиків та нуликів.
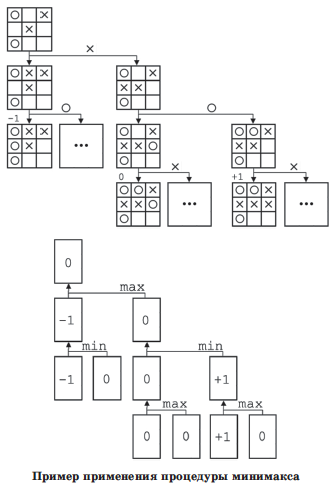
Нехай є процедура check_game, яка оцінює ситуацію на дошці, повертаючи 'X' або 'O', якщо у відповідного гравця поставлено 3 в ряд, або '-', якщо такого немає. Для листя нашого дерева ми можемо встановити їх статус (чийсь виграш або нічия).
Тепер розглянемо вузли дерева, що безпосередньо передують листю. Якщо хоча б один з листя призводить до виграшу гравця, ходу якого відповідає поточний вузол, то даний вузол також є виграшним. Вузол буде програшним тільки в тому випадку, якщо всі листи, в які він веде, є програшними. Таким способом можна помітити все вузли, що передують листю, і продовжувати поширювати цю інформацію вниз до кореня.
Зручніше уявити виграш комп'ютера як «+1», нічию як «0», а програш комп'ютера як «-1». Тоді для визначення статусу вузла, відповідного ходу комп'ютера, потрібно буде брати максимум, а для ходу противника - мінімум по всім дочірнім вузлів. Така процедура оцінки статусу вузлів, показана на наступному малюнку, називається процедурою минимакса. Вбудувати процедуру минимакса в породжує процедуру не представляє труднощі.
Необхідно відзначити існування в теорії ігор більш загального поняття - рівноваги Неша, відповідного таким стратегіям гравців, від яких жодному з них невигідно відхилятися, якщо цього не роблять і інші гравці.
Якщо породжує процедура відома і за допомогою процедури минимакса можна визначити оптимальний хід, в чому ж тоді проблема? Як уже неодноразово зазначалося вище, проблема - в NP-повноти. Іншими словами, повне дерево варіантів може вийти надзвичайно великих розмірів: найчастіше число вузлів зростає експоненціально з глибиною дерева, оскільки кожен вузол веде до деякого числа нових вузлів, кожен з яких, в свою чергу, знову веде до деякого числа нових вузлів. Наприклад, розмір дерева для шашок становить 10 ^ 40, для шахів - 10 ^ 120, а для го і зовсім неймовірне число - 10 ^ 400. Забавно, що часто, щоб підкреслити величину цих чисел, говорять про їх суттєве перевагу кількості атомів або елементарних частинок у Всесвіті, не цілком правомірно порівнюючи число об'єктів і число комбінацій станів об'єктів. Однак це порівняння стає виправданим, якщо говорити про класичні системах з масовою паралельною: навіть якщо кожен атом у Всесвіті буде окремим процесором, перебирати 10100 комбінацій в секунду, роботи всього Всесвіту протягом усього часу, що пройшов з моменту Великого вибуху, не вистачить, щоб зіграти ідеальну партію в го.
Дерево варіантів, заданий в неявній формі через правила гри, є як би невидимим для програми. Як щура, щоб обстежити справжній лабіринт, потрібно витратити якийсь час на дослідження кожної розвилки, за якої продовження шляху не видно, так і програмі потрібно витратити якийсь час (обчислювальні ресурси), щоб обстежити дерево варіантів і знайти потрібний шлях до перемоги.
Незважаючи на гадану елементарність, гра в «хрестики-нулики» навіть на поле 3 × 3 для дитини, не знайомої з нею, вимагає помітних розумових зусиль. Ця гра вимагає перебору варіантів на глибину 4-5, що близько до складності задачі про знаходження центру відрізка за допомогою циркуля і лінійки. Однак, «вирішивши» один раз «хрестики-нулики» на поле 3 × 3, ми будемо знати це рішення (шлях в «лабіринті» варіантів), і гра втратить для нас інтерес. Для «дорослих» інтелектуальних ігор така обмеженість не властива, оскільки весь простір пошуку в них не може бути обстежено протягом усього життя людини і навіть протягом всього часу існування цивілізації.
Що ж можна зробити, якщо все дерево породжене бути не може? З яких міркувань вибирати будь-якої хід? В області евристичного програмування термін «евристика» уточнюється як прийом, що дозволяє в ході перебору відсікати неперспективні гілки на дереві варіантів, що є помітно більш конкретним визначенням, ніж визначення евристики як прийому, що полегшує вирішення завдання.
Одна евристика вже неявно використовувалася при складанні дерева гри для «хрестиків-нуликів». На ньому показані всі початкові ігрові позиції, що не переводяться один в одного обертанням і дзеркальним відображенням. Іншими словами, використана евристика симетрії. Скільки існує варіантів гри, якщо не враховувати симетрії? Їх кількість - не більше ніж факторіал числа 9. Завдяки використанню симетрій це число зменшується на порядок. Однак для великих полів відносний виграш виявляється значно менше, так як вже після виконання кількох ходів симетричні продовження перестають існувати.
Симетрія є дуже загальною евристикою, проте не надто потужною, оскільки симетрія ігрової ситуації (навіть якщо вона є) дуже швидко порушується.
Можна уявити і більш складну (і більш приватну) евристику: вигідніше той хід, який потенційно може використовуватися в більшій кількості побудов трьох в ряд. З цієї евристики початково для «хрестиків» найвигіднішим є хід в центр, оскільки він може брати участь у чотирьох різних побудовах. Потім йдуть ходи в кути - для них число побудов дорівнює трьом. Для ходів під стінами це число всього лише два. Зрозуміло, що цієї евристики недостатньо, оскільки вона не враховує можливості противника (наприклад, завершити свою комбінацію).
Цілком природним є бажання оцінити вигідність ходу кількісно. На основі такої кількісної оцінки можна було б відсікати частина гілок в кожному вузлі дерева варіантів. І, дійсно, в евристичному програмуванні завдання евристик в формі (статичної) оцінює функції є найбільш поширеним.