Ектура комп'ютера уявлення чисел
Цілі числа є простими числовими даними, з якими оперує ЕОМ. Для цілих чисел існують два подання: беззнаковое (тільки для невід'ємних цілих чисел) і зі знаком. Очевидно, що негативні числа можна представляти тільки в знаковому вигляді. Цілі числа в комп'ютері зберігаються в форматі з фіксованою комою.
Подання цілих чисел в беззнакових цілих типах.
Для беззнакового уявлення все розряди осередки відводяться під уявлення самого числа. Наприклад, в байті (8 біт) можна уявити беззнакові числа від 0 до 255. Тому, якщо відомо, що числова величина є невід'ємне, то вигідніше розглядати її як беззнакову.
Подання цілих чисел в знакових цілих типах. Для уявлення зі знаком найстарший (лівий) біт відводиться під знак числа, інші розряди - під саме число. Якщо число позитивне, то в знаковий розряд поміщається 0, якщо негативне - 1. Наприклад, в байті можна уявити знакові числа від -128 до 127.
Прямий код числа. Подання числа в звичній формі "знак" - "величина", при якій старший розряд осередку відводиться під знак, а решта - під запис числа в двійковій системі, називається прямим кодом двійкового числа. Наприклад, прямий код двійкових чисел 1001 і -1001 для 8-розрядної комірки дорівнює 00001001 та 10001001 відповідно. Позитивні числа в ЕОМ завжди представляються за допомогою прямого коду. Прямий код числа повністю збігається із записом самого числа в комірці машини. Прямий код негативного числа відрізняється від прямого коду відповідного позитивного числа лише вмістом знакового розряду. Але негативні цілі числа не подаються у ЕОМ за допомогою прямого коду, для їх подання використовується так званий додатковий код. Додатковий код позитивного числа дорівнює прямому коду цього числа. Додатковий код негативного числа m дорівнює 2 k - | m |, де k - кількість розрядів в осередку. Як вже було сказано, при поданні невід'ємних чисел в беззнакову форматі все розряди осередки відводяться під саме число. Наприклад, запис числа 243 = 11110011 в одному байті при беззнакову поданні буде виглядати наступним чином:
Знаковий розряд Виникає питання: з якою метою негативні числа записуються у вигляді додаткового коду і як отримати додатковий код негативного числа? Додатковий код використовується для спрощення виконання арифметичних операцій. Якби обчислювальна машина працювала з прямими кодами позитивних і негативних чисел, то при виконанні арифметичних операцій слід було б виконувати ряд додаткових дій. Наприклад, при складанні потрібно було б перевіряти знаки обох операндів і визначати знак результату. Якщо знаки однакові, то обчислюється сума операндів і їй присвоюється той же знак. Якщо знаки різні, то з більшого по абсолютній величині числа віднімається менша і результату присвоюється знак більшого числа. Тобто при такому поданні чисел (у вигляді тільки прямого коду) операція складання реалізується через досить складний алгоритм. Якщо ж негативні числа представляти у вигляді додаткового коду, то операція додавання, в тому числі і різного знака, зводиться до з порозрядного додавання. Для комп'ютерного представлення цілих чисел зазвичай використовується один, два або чотири байти, тобто осередок пам'яті буде складатися з восьми, шістнадцяти або тридцяти двох розрядів відповідно.
Алгоритм отримання додаткового коду негативного числа. Для отримання додаткової k-розрядного коду негативного числа необхідно
модуль негативного числа уявити прямим кодом в k довічних розрядах;
значення всіх біт инвертировать: всі нулі замінити на одиниці, а одиниці на нулі (таким чином, виходить k-розрядний зворотний код вихідного числа);
до отриманого зворотного коду додати одиницю. Приклад: Отримаємо 8-розрядний додатковий код числа -52:
00110100 - число | -52 | = 52 в прямому коді
11001011 - число -52 в зворотному коді
11001100 - число -52 в додатковому коді Можна помітити, що уявлення цілого числа не дуже зручно зображувати у двійковій системі, тому часто використовують шістнадцяткове представлення:
Подання дійсних чисел в комп'ютері.
Для подання дійсних чисел у сучасних комп'ютерах прийнятий спосіб представлення з плаваючою комою. Цей спосіб представлення спирається на нормалізовану (експонентну) запис дійсних чисел. Як і для цілих чисел, при поданні дійсних чисел в комп'ютері найчастіше використовується двійкова система, отже, попередньо десяткове число повинно бути переведено двійкову систему.
Подання чисел з плаваючою комою. При поданні чисел з плаваючою комою частина розрядів осередку відводиться для запису порядку числа, інші розряди - для запису мантиси. По одному розряду в кожній групі відводиться для зображення знака порядку і знака мантиси. Для того, щоб не зберігати знак порядку, був придуманий так званий зміщений порядок. який розраховується за формулою 2 a-1 + ІП, де a - кількість розрядів, що відводяться під порядок. Приклад. Якщо істинний порядок дорівнює -5, тоді зміщений порядок для 4-байтового числа буде дорівнює 127-5 = 122.
Алгоритм уявлення числа з плаваючою комою.
Перевести число з p-ічной системи числення в двійкову;
уявити двійковечисло в нормалізованої експоненційної формі;
розрахувати зміщений порядок числа;
розмістити знак, порядок і мантиссу в відповідні розряди сітки.
Приклад: Уявити число -25,625 в машинному вигляді з використанням 4 байтового уявлення (де 1 біт відводиться під знак числа, 8 біт - під зміщений порядок, інші біти - під мантиссу).
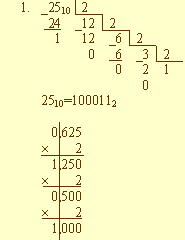
Можна помітити, що уявлення дійсного числа не дуже зручно зображувати у двійковій системі, тому часто використовують шістнадцяткове представлення:
Відповідь: C1CD0000.
Записати внутрішнє уявлення числа 250,1875 в формі з плаваючою крапкою.
1) Наведемо його в двійкову систему числення з 24 значущими цифрами: 250,187510 = 1111 1010. 0011 0000 0000 00002. 2) Запишемо в формі нормлізованного двійкового числа з плаваючою точкою: 0,1111 1010 0011 0000 0000 0000 * 102 1000. Тут мантиса, підстава системи числення (210 = 102) і порядок (810 = 10002) записані в двійковій системі. 3) Обчислимо машинний порядок в двійковій системі числення: Mp2 = 1000 + 100 0000 = 100 1000. 4) Запишемо подання числа в 4-х байтовой осередку пам'яті з урахуванням знака числа:
Шістнадцяткова форма: 48FA3000.
У семи довічних розрядах поміщаються двійкові числа в діапозоні від 0000000 до 1111111. Значить, машинний порядок змінюється в діапозоні від 0 до 127 (в десятковій системі числення). Всього 128 значень. Порядок, очевидно, може бути як позитивним так і негативним. Розумно ці 128 значень розділити порівну між позитивним і негативним значеніеямі порядку: від -64 до 63.
Машинний порядок зміщений відносно математичного і має тільки позитивні значення. Зсув вибирається так, щоб мінімального математичного значенням порядку відповідав нуль.
Зв'язок між машинним порядком (Мр) і математичним (р) в даному випадку виражається формулою: Мр = р + 64
Отримана формула записана в десятковій системі. У двійковій системі формула має вигляд: Mp2 = p2 +10000002 Для запису внутрішнього уявлення дійсного числа в 4-х байтовой осередку необхідно: 1) перевести модуль даного числа в двійкову систему числення з 24 значущими цифрами; 2) нормалізувати двійкове число; 3) знайти машинний порядок в двійковій системі числення; 4) з огляду на знак числа, виписати його подання до 4-х байтовому машинному слові.