Дещо про вигини залізничних рейок
Дещо про вигини залізничних рейок
Цікаве поруч. Якщо Вам доводилося їздити на потягах залізницею, то дивлячись на рейки Ви можливо замислювалися про те, як саме вони закругляются. Тобто мова йде про те, що ось їде поїзд по прямій, а потім починає повертати - як саме? Питання виявляється не зовсім тривіальним. Для початку нагадаю деякі відомості з курсу фізики. Сила, що діє на тіло (наприклад, залізничний вагон) пропорційна масі цього тіла помноженої на прискорення, з яким це тіло рухається. Я спеціально записав формулювання таким чином: як би навпаки, змінюючи причину і наслідок, тому що мова піде про неінерційні системи відліку. Зрозуміло, що якщо ми говоримо про штовхання санок на льоду, то потрібно говорити, що завдяки доданої силі санки починають прискоряться. Але коли мова йде про пасажира, який падає з полки через різке гальмування поїзда, то тут навпаки: ця невидима сила, яка зіпхнули пасажира, викликана прискоренням поїзда, в якому цей пасажир перебував. Так ось, на самому початку розвитку залізниць, коли швидкості поїздів були маленькими, питання про те як скруглять рейки на поворотах не був так актуальне. Можна було просто робити перехід від прямого рейки до рейки, який є частиною окружності з потрібним радіусом повороту R0.
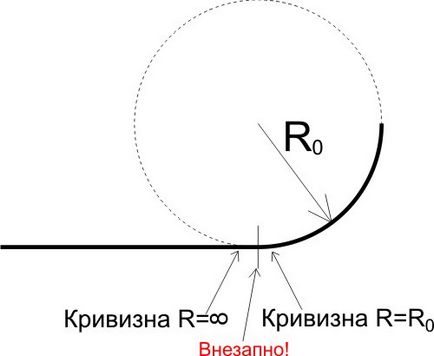
Однак, такий підхід небезпечний тим, що при русі по такому залізничного полотна в момент переходу від прямого рейки до досить сильно закругленому на поїзд починає різко діяти відцентрова сила. Тобто по суті справи при русі по такій кривій відбувається удар в сторону. Нагадаю, що відцентрова сила дорівнює:
(1)
де - швидкість поїзда, - радіус кривизни. Хочу зазначити, що радіус кривизни, кривизна (кривизна = 1 / радіус кривизни) - поняття, які застосовуються не тільки до кола, а й взагалі до будь-якої хитромудрої кривої. У довільній кривій, на відміну від окружності, радіус кривизни різний для різних точок даної кривої. Як знайти радіус кривизни для довільної точки кривої? Потрібно взяти дві точки (червоні точки на малюнку нижче) на кривій поруч з потрібною нам (жовта), провести через ці точки дотичні (червоні) до кривої, потім через ці ж точки провести перпендикуляри (сині) до дотичним. Відстань від точки перетину перпендикулярів до кривої (зелений відрізок) і буде радіусом кривизни.
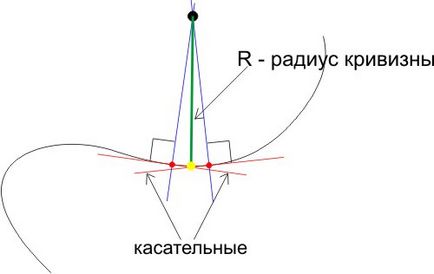
Природно, Новомосковсктелі не обізнані з диференціальним численням можуть задатися питанням: а конкретно до якоїсь точки кривої (жовта на малюнку) потрібно міряти відстань від точки перетину перпендикулярів? Відповідь така: якщо відстань між червоними крапками (точками, в яких ми проводимо дотичні до кривої) стремить до нуля, то можна брати в якості жовтої точки на кривій будь-яку з червоних, вони адже всі три будуть нескінченно близько один до одного. Отже, саме цей радіус кривизни входить в формулу (1) для відцентрової сили. І звідти видно, що для прямої, у якій нескінченний радіус кривизни, відцентрова сила дорівнює нулю. Тобто при русі поїзда по прямому шляху, різко переходить в дугу окружності, отримуємо наступну залежність відцентрової сили від часу:
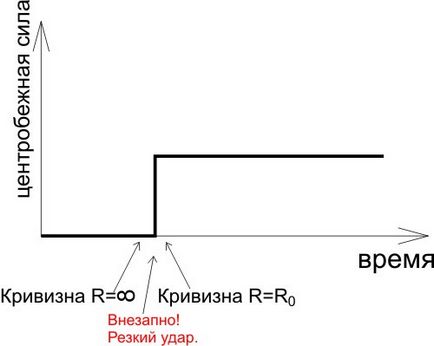
Видно, що сила з'являється раптово. А це погано, раптова сила по простому називається ударом, такий удар може сильно качнути вагон і спровокувати аварію. Тому при прокладці залізничних шляхів роблять так, щоб відцентрова сила при русі по кривій наростала поступово:
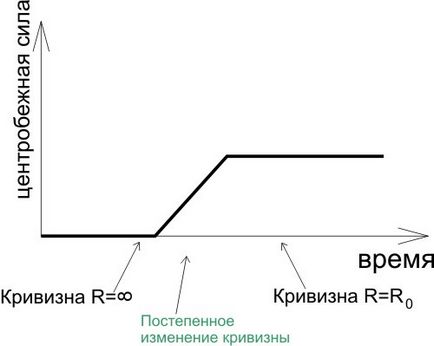
Тобто між прямим ділянкою з нескінченним радіусом кривизни і дугою кола роблять перехідну криву, радіус кривизни якої змінюється від нескінченного до кінцевого. Наприклад, це може бути крива, яка задається виразом вигляду:, що є апроксимацією кривої, яка називається «клотоїда». Клотоїд - це така крива, в якій кривизна (кривизна =) пропорційна пройденого шляху (при повороті кермо повертається з постійною швидкістю). Повороти автомобільних швидкісних трас теж роблять по клотоїди, це, як стверджує вікіпедія, дозволяє проходити такі повороти практично без зниження швидкості.
Ось таким способом мат.аналіз і диференціальна геометрія стають корисними в народному господарстві 🙂
Якщо вам сподобався матеріал, будь ласка, поділіться ним з друзями:
Немає схожих постів