Число різних k-елементарних підмножин n-елементарного безлічі - студопедія
Подивимося тепер, скільки існує різних підмножин з k елементів у множині, що складається з п елементів (k <п).
ТеоремаЧісло різних k-елементних підмножин n-елементарного безлічі одно
де скорочення п! = П * (п - 1) *. * 3 * 2 * 1 називається факторіалом числа n (читається n-факторіал). Причому 0! = 1. А скорочення.
Доведення. Щоб побудувати k -елементное підмножина безлічі А, необхідно до (k - 1) -елементному безлічі приєднати один з п - k + 1 елементів, які не входять в цей підмножина. Оскільки число (k - 1) -елементних підмножин одно, І кожне з цих підмножин можна зробити k-елементним п - k + 1 способами, за основним правилом комбіна-Ториком отримуємо число * (n - k + 1) підмножин. Однак не всі ці підмножини будуть різними, оскільки будь-яке k -елементарное підмножина можна також побудувати k способами. отже,
Оскільки - число одноелементні підмножин безлічі А - одно n, то
Довільний k -елементное підмножина безлічі А називається комбінацією, або вибіркою, а число - числом комбінацій або сполучень з n елементів по k елементів.
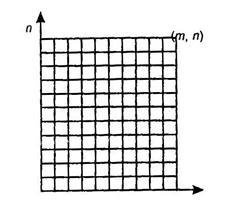
Біноміальні коефіцієнти мають цікаву геометричну Інтерпро-цію. Нехай маємо прямокутну шахову дошку розміром m на n, раз-ня на координатної площині. Ця дошка складається з m * n елементарних квадратів, розділених n - 1 горизон-тальної лінією і m - 1 вертикальної. Визначимо, скількома різними найкоротшими шляхами можна потрапити з точки (0, 0) в точку (m. N) на цій дошці.
Кожен найкоротший шлях, що веде з точки (0, 0) в точку (m, n), складається, очевидно, з m + n сторін елементарних квадратів, серед яких m гори-зонтальним і n вертикальних. Ці шляхи відрізняються між собою тільки 1 числом вертикальних і горизонтальних сторін. Значить, загальна кількість шляхів дорівнює числу способів, якими з т + n сторін можна вибрати n верти-Кальний, тобто це число дорівнює.
Зауважимо, що можна було б вести підрахунок не по вертикальних сторонах,
а по горизонтальних. Тобто, існує різних найкоротших шляхів і, отже, справедливо рівність:
Дане рівність має назву «формула симетрії».
З цієї формули маємо наслідок:
має назву «формула складання». Доведемо даний наслідок.
Збірна команда університету з волейболу налічує 15 осіб. Скільки різних варіантів повинен розглянути тренер перед грою, щоб заявити список гравців на гру?
Рішення: Число гравців волейбольної команди одно шести. Значить, число всіх можливих варіантів - це число різних підмножин, що складаються з шести елементів у множині з п'ятнадцяти елементів. Отже, за теоремою 2 маємо