Аналітична геометрія (2) - навчальний посібник, сторінка 2
Приклад 2 (знаходження відстані між двома точками)
Знайти відстань між точками
Координати точок задані в полярних координатах, а вираз для знаходження отримано для точок, заданих в ПДСК, а тому, перш за все, необхідно висловити координати точок в ПДСК.
З таблиці взаємозв'язку полярних і декартових координат отримуємо, що для точки
або, координати точки М в ПДСК -.
Аналогічно знаходимо і координати точки N:
або, координати точки N в ПДСК -.
А ось тепер, остаточно, використовуючи результат «відстань між двома точками на площині», отримуємо, що
Обчислення площі довільного трикутника в ПДСК
Нехай в ПДСК заданий довільний трикутник ABC. А (x 1. y 1), B (x 2. y 2) і C (x 3. y 3), тоді площа трикутника S ABC визначається виразом
Оскільки точки можуть бути пронумеровані в довільному порядку, знак визначника може змінюватися. В силу чого існує правило: результат береться за абсолютною величиною (по модулю).
Розподіл відрізка в даному відношенні
Перш за все, про сенс виразу «поділ відрізка в даному відношенні».
Нехай точка В ділить відрізок А1 А2 (див. Рис.7)
Тоді, тобто якщо то . Але якщо відрізок «прочитати» по-іншому: чи не А1 А2. а А2 А1. то
Звідки важливий висновок. при розбитті відрізка щодо λ, важливо як влаштована дріб
тобто важливо, в якому напрямку Новомосковскется відрізок: А1 А2. або А2 А1.
Координати точки, що ділить відрізок в даному відношенні
Слідство. якщо точка В ділить відрізок А1 А2 навпіл, тобто λ = 1 (чому?), то
Приклад 3 (про знаходження координат точки, що ділить відрізок в даному відношенні)
Відомо, що точки А (- 2; 5) і В (4; 17) - кінці відрізка АВ. Усередині цього відрізка знаходиться точка С, відстань якої від А в два рази більше відстані від В. Знайти координати точки С (x; y).
За умовою завдання, звідки
Приклад 4 (про координати точки перетину медіан)
Трикутник АВС заданий координатами вершин: А (x 1; y 1), B (x 2; y 2) і C (x 3; y 3). Знайти координати точки перетину медіан трикутника.
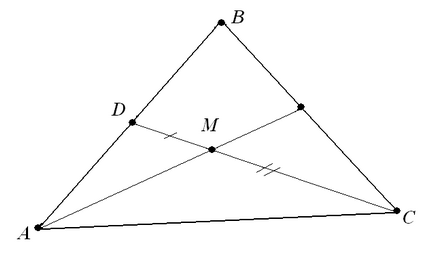
Для знаходження координат точки М використовує властивість точки перетину медіан: ця точка розбиває відрізок З D щодо 2: 1, рахуючи від вершини С,
рівняння лінії
Рівнянням даної лінії назвемо таке рівняння F (x; y) = 0, якому задовольняють координати x і y будь-якої точки, що належить цій лінії, і не належать точки, що не задовольняють рівняння (задовольняє рівняння - значить координати, точки, будучи підперті в рівняння, звертають рівняння в тотожність).