Векторна графіка
Векторне подання, на відміну від растрової графіки, визначає опис зображення у вигляді ліній і фігур, можливо, з зафарбованими областями, заповнюється-мимі суцільним або градієнтним кольором. Хоча це може здатися більш складним, ніж використання растрових масивів, але для багатьох видів зображень використання математичних описів є більш простим способом.
У векторній графіці для опису об'єктів використовуються комбінації комп'ютерах терни команд і математичних формул для опису об'єктів. Це дозволяє раз-особистим пристроїв комп'ютера, таким як монітор і принтер, при малюванні цих об'єктів обчислювати, де необхідно поміщати реальні точки.
центр - 50, 70; радіус - 40;
лінія: колір - чорний, товщина - 0.50;
Даний приклад показує основна перевага векторної графіки - опис об'єкта є простим і займає мало пам'яті. Для опису цієї ж кола засобами растрової графіки треба було б запам'ятати кожну окрему точку зображення, що зайняло б набагато більше пам'яті.
Крім того, векторна графіка в порівнянні з растровою має такі переваж-вин:
простота масштабування зображення без погіршення його якості;
незалежність обсягу пам'яті, необхідної для зберігання зображення, від обраний-ної колірної моделі.
Недоліком векторних зображень є їх деяка штучність, зак-Лючано в тому, що будь-яке зображення необхідно розбити на кінцеве безліч складових його примітивів.
Розглянемо докладніше способи представлення різних об'єктів в векторної графіки.
Крапка. Цей об'єкт на площині представляється двома числами (х, у), вказую-ські його положення щодо початку координат.
Пряма лінія. Їй відповідає уравненіеу = kx + b. Вказавши параметриk і b, завжди можна відобразити нескінченну пряму лінію у відомій системі коор-ДИНАТ, тобто для завдання прямої достатньо двох параметрів.
Відрізок прямої. Він відрізняється тим, що вимагає для опису ще двох парамет-рів - наприклад, коордінатx іy початку і кінця відрізка.
Крива другого порядку. До цього класу кривих відносяться параболи, гіперболи, еліпси, кола, тобто всі лінії, рівняння яких містять ступені не вище другої. Крива другого порядку не імеетточек перегину. Прямі лінії є всього лише окремим випадком кривих другого порядку.
Крива третього порядку. Відмінність цих кривих від кривих другого порядку полягає в можливу наявність точки перегину. Наприклад графік функцііу = х 3 має точ-ку перегину на початку координат. Саме ця особливість дозволяє зро-лать криві третього порядку основою відображення природних об'єктів в век-битим графіку. Наприклад лінії вигину людського тіла вельми близькі до кривим третього порядку. Всі криві другого порядку, як і прямі, є окремими випадками кривих третього порядку.
Криві Безьє. Це особливий, спрощений вигляд кривих третього порядку (див. Рис. 2). Метод побудови кривої Безьє (Bezier) заснований на використанні пари касатель-них, проведених до відрізка лінії в її закінченнях. Відрізки кривих Безьє описи-ються вісьмома параметрами, тому працювати з ними зручніше. На форму лінії впливає кут нахилу дотичної та довжина її відрізка. Таким чином, дотичні відіграють роль віртуальних "важелів", за допомогою яких керують кривої.
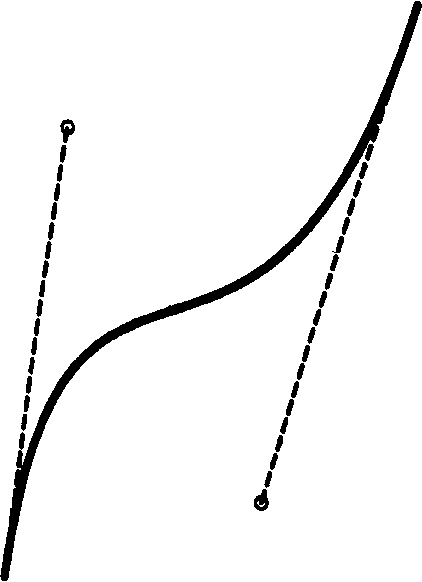
Мал. 2. Крива Безьє
Растрова і векторна графіка існують не відокремлено один від одного. Так, вектор-ні малюнки можуть включати в себе і растрові зображення. Крім того, векторні і растрові зображення можуть бути перетворені одна в одну - в цьому випадку говорять про конвертацію графічних файлів в інші формати. Досить просто виконується перетворення векторних зображенні в растрові. Не завжди можна здійснити Перетворюва-ня растрової графіки у векторну, так як для цього растрова картинка повинна содер-жати лінії, які можуть бути ідентифіковані програмою конвертації (типу CorelTrace в складі пакету CorelDraw) як векторні примітиви. Це стосується, наприклад; високоякісних фотографій, коли кожен піксель відрізняється від сусідніх.