Вантажні автомобільні перевезення (1) - книга, сторінка 80
побудувати для завантаженої клітини, по якій визначені два по-потенціалу, контур так, щоб всі його кути лежали в завантажених клітинах;
кути контуру позначити поперемінно знаками «плюс» і «мінус». Кутку, який лежить в завантаженої клітці, для якої побудований контур, присвоюється знак «плюс»;
виявити найменшу завантаження в клітинах, зайнятих кутами зі знаком «плюс», відняти її з усіх клітин і додати в усі клітини, зайняті кутами зі знаком «мінус».
В результаті таких дій число завантажених клітин скоротиться. При цьому раніше знайдене рішення або покращиться, або залишиться тим самим.
Якщо число завантажених клітин при складанні базисного плану окажетсяменьше, ніж т + п-1, то недостатня кількість клітин загру-жают нулями. Завантажувати слід ті клітини, які лежать на перетнути-ванні рядків і стовпців, які не мають потенціали, з рядками або стовп-цями, для яких потенціали вже визначені і мають найменші значення показника критерію оптимальності.
Додаткові умови при вирішенні транспортних задач ме-тодом потенціалів. Пропозиція більше попиту. Умови завдання записуються в таблицю, в яку вводиться фіктивний стовпець Р з обмеженням по попиту, рівний різниці між пропозицією і попитом. Так як вантаж нікуди не вивозиться, то в кутах клітин стовпця Р ставляться нулі. Завдання вирішують за алгоритмом методу потенціалів, рас-сматривая стовпець Р як споживач вантажу.
Якщо попит перевищує пропозицію, ™ подібним об-разом такі завдання вирішувати не можна. У цьому випадку один з споживачів не отримає вантажу, а неотримання вантажу різними одержувачами надає неоднаковий вплив на кінцеві результати роботи цих підприємств.
Заборона кореспонденції. Якщо необхідно з яких-небудь при-чинам накласти заборону на перевезення вантажу з пункту A1 в пункт В1. то для цього достатньо замість реального елемента цільової матриці, що стоїть в клітці А1 В1. поставити дуже велику величину М, яка більше лю-бого наперед заданого числа, наявного в даній задачі.
Обов'язкова поставка. Якщо з пункту Аi - в обов'язковому порядку не-обходимо перевезти в пункт Bj якийсь обсяг вантажу, то в цьому випадку ве-личина обов'язкової поставки віднімається від суми попиту і суми пред-ложений і при вирішенні завдання не враховується. При визначенні оконча-ного результату витрати, пов'язані з обов'язковим обсягом перевезень, додаються до отриманого оптимального варіанту.
Відкрита модель виникає у випадках, коли відсутня ка-кая-небудь з груп обмежень - попит або пропозицію. Це означає, що будь-який споживач може взяти всю суму наявних у постачальників матеріалів або будь-який з постачальників може задовольнити попит всіх споживачів даного матеріалу.
Рішення завдання. Якщо відсутні обмеження за пропозицією, то обмеження щодо попиту в кожному стовпчику таблиці переносяться в кліть-ки з оптимальним елементом цільової матриці даного стовпця, а при від-присутність обмежень за попитом - в клітку кожного рядка.
Ознаки наявності альтернативних рішень. При вирішенні завдань методом потенціалів може бути, що при одному і тому ж значенні цільової функції є кілька базисних планів з різними варіантами вантажопотоків. Ознакою наявності альтернативного оптимального плану при вирішенні задач методом потенціалів є наявність рівності суми потенціалів з елементом цільової матриці в одній або декількох вільних клітинах.
8.4. маршрутизації ПЕРЕВЕЗЕНЬ
Маршрутизація перевезень - це складання маршрутів руху рухомого складу або його порядок проходження між пунк-тами виробництва і споживання. Маршрутизацію перевезень виконуємо-ють для однорідних вантажів, що вимагають для перевезення однотипний під-Віжн склад. При маршрутизації перевезень враховується безліч обмежень, що викликаються конкретними умовами роботи транспорту: обсяги перевезень постачальників і споживачів, характер вантажів, час їх доставки, структура парку рухомого складу і його наявність, режим роботи автотранспортних підприємств і вантажно-розвантажувальних пунктів, режим роботи водіїв, пропускна можливість вантажно-розвантажувальних пунктів і дорожньої мережі, значення цільової функції і ін.
Методи маршрутизації перевезень поділяються на маршрутизацію перевезень помашінних відправок та маршрутизацію перевезень дрібних партій вантажів.
Залежно від використання математичних-ського апарату вони діляться на методи, засновані на моделях ма-тематичного програмування, і на методи, засновані на алго-ритмах завдань теорії розкладів.
Методи першого класу діляться на дві групи. До пер-виття групи належать завдання, в яких за певних поїздки з вантажем визначаються потоки руху автомобільного рухомого складу без вантажу.
Недоліки цього методу: не забезпечується облік всіх ограниче-ний і параметрів, що існують в реальній системі (час в наряді, закріплення автомобілів за клієнтурою і т. Д.);
виникає необхідність коригування плану вручну (склад-ня графіків руху, графіка роботи вантажно-розвантажувального пункту), що іноді призводить до відхилень від отриманого варіанту.
Методи другої групи розглядають маршрути руху як технологічні способи використання ресурсів з певними «цінами», і задаються стовпці матриці умов. Змінними є-ються інтенсивності вантажопотоків по маршрутам.
Переваги (порівняно з першим методом): можливість обліку багатьох обмежень, висунутих практикою; виключення ручних операцій при складанні оперативного плану.
велика розмірність завдань, що визначає труднощі рішення;
не враховується наявність черг в пунктах виконання вантажно-розвантажувальних робіт (ПРР);
алгоритми мають недостатнє швидкодію для оперативного управління перевізним процесом в реальному режимі часу.
Методи другого класу побудовані на використанні ап-Параті теорії розкладів. Етапи транспортного процесу (навантаження, транспортування, розвантаження, подача рухомого складу) подаються у вигляді «робіт». Рухомий склад та пости ПРР виступають як «прилади-ри», призначені для виконання «робіт». В результаті рішення задачі визначається розклад виконання «робіт» (розподіл ре-сурсів між роботами і черговість виконання робіт).
відсутні алгоритми точного рішення задач теорії розкладів через велику розмірності.
В даний час відомі наступні наближені методи ре-шення завдань теорії розкладів:
методи випадкового пошуку;
методи ситуаційного управління;
методи, засновані на евристичних процедурах скорочення раз-мірності завдання.
Методи випадкового пошуку побудовані на використанні процедури Монте-Карло. З отриманого безлічі рішень вибирає-ся найкраще, згідно заданому критерію оптимальності. Отримано-ні цим методом рішення зазвичай знаходяться на рівні рішень, при-Німан досвідченим диспетчером. З цієї причини вони не знайшли широ-кого застосування.
Моделі методів теорії ситуаційного управ-ня певним чином формалізують реальні системи, які працюють в діалоговому режимі з ЕОМ і можуть «навчатися» на досвіді експертів (диспетчерів). Так як модель переймає досвід людини, то після «навчання» вирішує завдання на рівні брали участь екс-пертів. Потрібна велика час на «навчання» ЕОМ; так само як і має місце складність алгоритмічної і програмної реалізації.
Методи, засновані на евристичних процеду-рах скорочення розмірності задачі, полягають в наступному. Про-процес складання маршрутів руху ділиться на кілька кроків. На кожному кроці вибирається «робота» для завантаження незайнятого «приладу». Вибір здійснюється з деякої кількості «робіт», які можуть бути виконані даним «приладом». Наявність свободи вибо-ра «робіт» обумовлює існування певного безлічі планів, які відрізняються один від одного величиною деяких показу-телей (простої «приладів», загальна тривалість виконання за-даних «робіт» і т. Д.). Функції переваги є формальну оцінку прийнятого рішення на конкретному кроці фор-мування оперативного плану.
Використання функцій переваги дозволяє сформувати план, близький до оптимального, не "переглядаючи» інших можливих рі-ний. В якості опції переваги можуть виступати тривалість виконання чергового етапу обслуговування і ін.
Для досягнення оптимальності отриманих планів використовують комбінацію функцій переваги як рішення комбінаторних завдань як в вигляді послідовності функцій переваги, так і у вигляді узагальненого показника.
Найбільше застосування для формування маршрутів перевезень знаходить метод «суміщеної матриці», коли при відомих поїздки з вантажем визначається рух рухомого складу без вантажу. Цей метод передбачає, що план поставок виконується сукупністю будь-яких маятникових і кільцевих маршрутів незалежно від їх протя-ності, числа ланок і без урахування подачі і повернення автомобілів. Необхідна умова - число автомобілів, що прибувають в пункт по-грузки, повинна дорівнювати числу автомобілів, що виходять з цього пункту.
Завдання формулюється так: мінімізувати хо-Лост пробіги
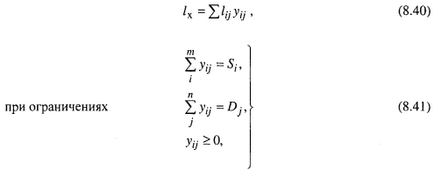
де: yij - число їздець без вантажу з j пункту вивантаження в i пункт навантаження. Розглянемо застосування цього методу на прикладі.
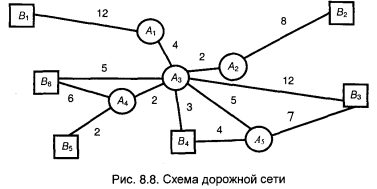
Раціональне закріплення споживачів вантажів за постачальниками приведено в табл. 8.9-8.11. Найкоротша відстань між пунктами вка-зано в табл. 8.12. Всі перераховані будівельні матеріали можна перевозити на одному і тому ж типі рухомого складу.
Необхідно так організувати перевізний процес, щоб коефіцієнт вико-вання пробігу рухомого складу мав максимально можливу вели-чину.
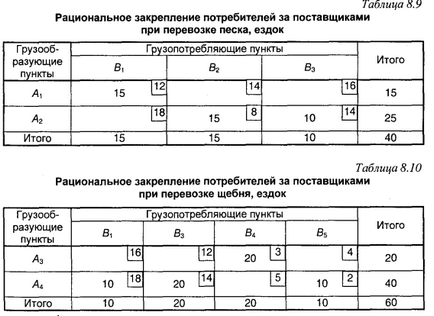

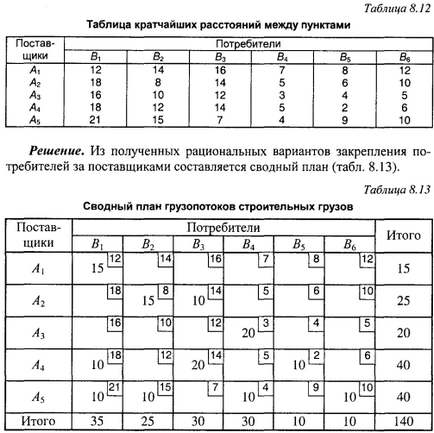
Одним з математичних методів визначається раціональний план руху автомобілів з пунктів вивантаження вантажів в пункти навантаження (табл. 8.14).
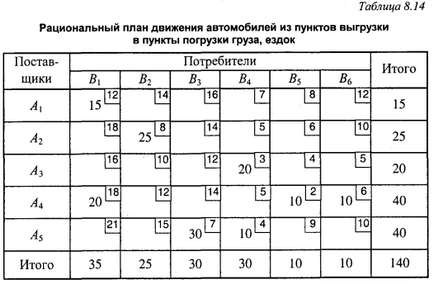
Для складання маршрутів можна користуватися методом «совме-щенной матриці». Сутність цього методу полягає в тому, що в одну матрицю записуються дані про поїздку з вантажем і неодружених поїздки (табл. 8.15).
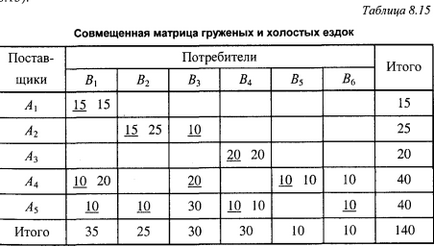
Щоб відрізняти навантажені їздки від неодружених, бажано одні з них виділити (підкреслити, обвести кружком, записати іншим кольором і т. Д.) - У нашому прикладі поїздки з вантажем підкреслені. Якщо в клітці будуть два записи, то це вказує на наявність маятникового маршруту, величи-на вантажопотоку якого визначається меншою цифрою.
Після того як будуть виявлені митників маршрути, в клітинах таблиці залишиться тільки по одній цифрі (табл. 8.16).
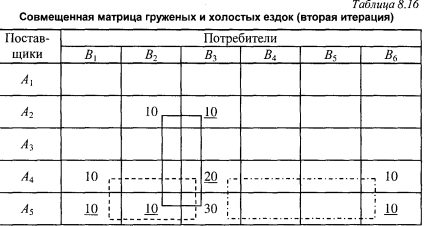
Для кожної клітини табл. 8.16, завантаженої їздки з вантажем, будується контур (маршрут руху), вершини якого поперемінно перебувають в клітинах, завантажених навантаженими і холостими поїздки.
Величина вантажопотоку кожного маршруту визначається найменшою величиною навантажених їздець. Визначення кільцевих маршрутів продов-жается до тих пір, поки не залишиться жодної завантаженій клітини.
У табл. 8.17 приведені раціональні маршрути руху під-Віжн складу, певні з умов нашої задачі.
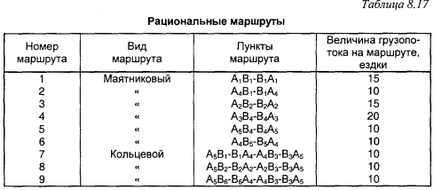
Для складання схем маршруту руху рухомого складу необ-обхідно визначити початковий і кінцевий пункт кожного маршруту.
Раціональний вибір початкового та кінцевого пунктів маршруту дозволяє скоротити пробіг рухомого складу без вантажу за рахунок того, що в останньому обороті рухомого складу по маршруту з суми загального пробігу випадає ділянку від останнього пункту вивантаження до першого пункту навантаження. У маятникових маршрутах може бути тільки один варіант початкового та кінцевого пунктів мар-Шрута. При виконанні кільцевих маршрутів початок маршруту може бути з будь-якого пункту навантаження, т. Е. Число варіантів дорівнює числу вантажних пунктів в маршруті.
За критерій оптимальності при виборі началь-ного пункту маршруту приймається мінімум суми нульового пробігу з непродуктивною (холостим) пробігом рухомого соста-ва, т. Е.мінімізіровать
де: 1 "х - пробіг рухомого складу без вантажу від останнього пункту вивантаження до першого пункту навантаження, км;
loi - нульовий пробіг при i початковому пункті маршруту, км.
Σlxi - сума неодружених пробігів на ділянках маршруту, км