Умова жорсткості
Умова жорсткості стрижня
O` (погонний кут закр.) = Mкрmax / G * Jро<[O]
Критерії пластичності і руйнування. Перша, друга, третя і четверта теорії міцності. Торію Мора. Загальні відомості про різні гіпотези міцності і пластичності. Загальний план рішення задачі про перевірки міцності.
У загальному випадку небезпечне напружений стан елемента конструкції залежить від співвідношення між трьома головними напруженнями (s1, s2, s3). Тобто строго кажучи, для кожного співвідношення потрібно експериментально визначати величину граничної напруги, що нереально. Тому було прийнято такі методи розрахунку міцності, які дозволяли б оцінити ступінь небезпеки будь-якого напруженого стану по напрузі розтягування - стиснення. Вони називаються теоріями міцності (теорії граничних напружених станів).
1-ша теорія міцності (теорія максимальних нормальних напружень) Встановив Кулон: При будь-якому напр. стані крихке руйнування буде, якщо макс. норм. напруга досягає граничного значення для данногоматеріала Головний недолік: не враховуються два інших головних напруги. Підтверджується досвідом тільки при розтягуванні вельми крихких матеріалів (скло, гіпс). В даний час практично не застосовується.
сигма max<сигма пред.(экспиремент на растяжение)
сигма екв. = сигма гл. <[сигма]доп.
2-а теорія міцності (теорія максимальних відносних деформацій): При будь-якому напр. сос-ії крихке разр. буде якщо макс. відносить. дефор-ії досягнутий попер. знач.
Умова разр-ия: Епсілон max = Епсілон ін.
ус-ие міцності: σекв. = σ1-V (ню) * (σ2 + σ3)<[σ]доп.
3-тя теорія міцності (теорія максимальних дотичних напружень): При При будь-якому напр. сос-ії пластич. разр. буде якщо макс дотичні напруження досягнуть попер. стану tmax = tпред. tmax = σ1-σ3 / 2, умова міцності: σеквIII = σ1 - σ3≤ [σ]. Основний недолік - не враховує вплив s2.
При плоскому напруженому стані: sеквIII = £ [s]. При sy = 0 отримуємо Широко використовується для пластичних матеріалів.
4-я теорія міцності (енергетична теорія) При будь-якому напр. стані разр. буде якщо питома робота зі зміни форми досягне попер. значення.
Враховує, все три головних напруги.
Широко використовується для пластичних матеріалів.
Теорія міцності Мора Отримано на основі кіл напруг Мора. Використовується при розрахунках тендітних матеріалів, у яких допустимі напруження на розтяг [sp] і стиснення [SС] не однакові (чавун).
Для пластичних матеріалів [sp] = [SС] теорія Мора перетворюється в 3-ю теорію.
Коло Мора (коло напруг). Координати точок кола відповідають нормальним і дотичним напруженням на різних майданчиках. Відкладаємо від осі s з центру З промінь під кутом 2a (a> 0, то проти час.стр.), Знаходимо точку D,
координати якої: sa, ta. Можна графічно вирішувати як пряму, так і зворотну задачі.
Загальний план рішення задачі про перевірки міцності:
Перевіряємо умову міцності (Для крихких матеріалів ісп 1, 2 теорію міцності і Теорію міцності Мора; Для пластичних матеріалів 3ая і 4ая теорія міцності)
Визначаємо дійсний коефіцієнт запасу міцності. (N (дійств.))
Знаходимо небезпечне перетин.
для 1ой і 2 ой теор. Міцності: небезпечне перетин - це майданчик перпендикулярна першому головному напрямку
для 3ей і 4ой теор. Небезпечне перетин - плозадка на якій дійств. Істинний максимум дотичних напружень. І для 4 оп.сеч - октаедричні майданчик, тобто одно нахилена по всьому 3ем осях.
Чистий і поперечний вигин. типи опорних зв'язків. визначення спірних реакцій. Внутрішні зусилля при плоскому вигині і зв'язок між ними. Епюри перерізують сил і згинальних моментів. Диференціальні залежності междуq, MіQ.
Якщо при прямому або косому вигині в поперечному перерізі бруса діє тільки згинальний момент, то відповідно є чистий прямий або чистий косою вигин. Якщо в поперечному перерізі діє також і поперечна сила, то є поперечний прямий або поперечний косою вигин.
Стрижні, які працюють переважно на вигин, називають балками (застосовуються в конструкціях будівель різноманітного призначення, мостах, у вигляді під кранових балок виробничих будівель і т. Д.). Вони мають простоту конструкції, виготовлення і надійністю в роботі.
Шарнірно'подвіжная опора. Ця опора є пристроєм, що допускає переміщення опорного перетину паралельно опорній площині і поворот його у вертикальній площині щодо осі циліндричного шарніра. Це пристрій не дає можливості переміщатися в напрямку накладеної зв'язку по вертикалі. Реакція шарнірно_подвіжной опори VA спрямована уздовж опорної зв'язку.
Шарнірно'неподвіжная опора. Ця опора не допускає зсувів опорного перетину ні в поздовжньому, ні в поперечному напрямках, проте допускає поворот цього перерізу відносно шарніра. Шарнірно нерухома опора являє собою опору з двома зв'язками, які зручно прикладати у напрямку осі балки і перпендикулярно осі балки. У цій опорі з'являються дві складові опорної реакції: HA і VA.
Жорстке закріплення або закладення. Ця опора не допускає повороту опорного перетину і переміщення його ні в якому направ_леніі - на це перетин накладені три зв'язку: вертикальна VA. горизонтальна НА. складові опорної реакції, і вигинає момент МА.
Якщо в балці перетином, які мають вертикальну вісь, зовнішнє навантаження і реактивні зусилля лежать в одній площині, що збігається з віссю перерізу, то балка будетізгібаться в тій же площині. Такий вигин називають плоским.
Нехай при плоскому вигині зовнішнє навантаження перпендикулярна поздовжньої осі балки, тоді в поперечних перетинах балки виникають лише поперечна сила і згинальний момент, а поздовжня сила дорівнює нулю. Такий вигин називають поперечним.
Диференціальні залежності між q, M і Q.
Нормальні напруги при чистому вигині - гіпотеза плоских перетинів, нейтральна вісь, визначення напружень. Максимальні нормальні напруження при згині, момент опору перерізу, равнопрочние балки.
Гіпотеза плоских перетинів: перетину, перпендикулярні осі стержня і плоскі до деформації залишаються такими ж і після прикладення навантаження.
Від дії згинального моменту в поперечних перетинах балки виникають нормальні напруження, що визначаються за формулою
,де М - згинальний момент в перерізі;
I - момент інерції поперечного перерізу балки відносно нейтральної осі;
у - відстань від нейтральної осі до точки, в якій визначаються напруги.
З формули (8.1), нормальні напруги в перетині балки по її висоті лінійні, досягаючи максимального значення в найбільш віддалених точках від нейтрального шару.
,де W - момент опору поперечного перерізу балки відносно нейтральної осі. В основі гіпотези плоских перетинів лежить припущення, що і всередині стрижня деформації мають такий же характер, як на поверхні. Отже, перетину, плоскі і нормальні до осі стержня до деформації, залишаються плоскими і нормальними до його осі і після деформації. В цьому і полягає сенс гіпотези плоских перетинів.
Нейтральна вісь - лінія в поперечному перерізі згинається балки, в точках якої нормальні напруги, паралельні осі балки, дорівнюють нулю. Нейтральна вісь ділить перетин на дві частини, в одній з яких діють розтягують нормальні напруги, а в іншій - стискають.
Осьовим моментом опору називається відношення моменту інерції щодо даної осі до відстані від осі до найбільш віддаленої точки поперечного перерізу
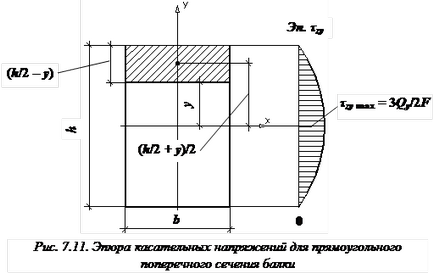
Дотичне напруження при згині. Формула Журавського. Епюри дотичних напружень в прямокутному і двотаврового перетину.
Дотичне напруження в будь-якій точці поперечного перерізу (рис. 2) визначається, як і парне напругу, що виникає в поздовжньому перетині, по формулі Журавського; Txz =
,де - поперечна сила в перерізі; - статичний момент відсіченої частини, b - ширина поперечного перерізу на рівні досліджуваної точки, - момент інерції всього перерізу відносно нейтральної осі.
Формула Журавського дозволяє визначити дотичні напруження при згині, що виникають в точках поперечного перерізу балки, що знаходяться на відстані від нейтральної осі x. Формула Журавського для дотичних напружень:
,
де Q - поперечна сила; S * x - статичний момент відтятою частини поперечного перерізу відносно осі х. F * - площа відтятою частини поперечного перерізу, yc - відстань від центру відтятою частини поперечного перерізу до осі х. Jx - головний осьовий момент інерції повного перетину, by - ширина перетину в тій точці, для якої знаходиться напруга.