Тригонометричні функції, енциклопедія Навколосвіт
ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ - один з класів елементарних функцій.
Функція у = cos х.
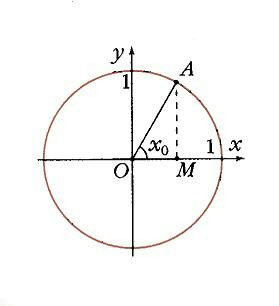
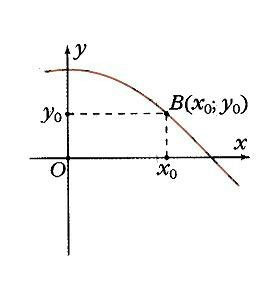
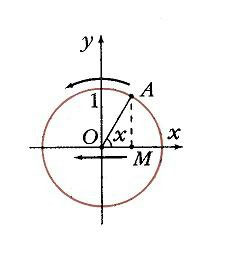
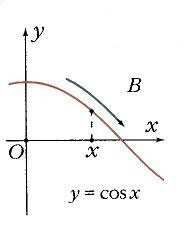
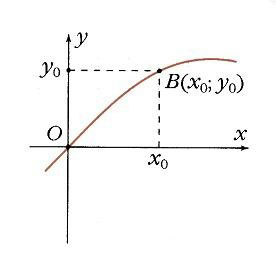
Якщо побудувати одиничну окружність з центром на початку координат, і задати довільне значення аргументу x0 і відрахувати від осі Ox кут x0, то цього кутку на одиничному колі відповідає певна точка A (рис. 1) а її проекцією на вісь Ох буде точка М. Довжина відрізка ОМ дорівнює абсолютній величині абсциси точки A. Даному значенню аргументу x0 порівнювати значення функції y = cos x0 як абсциси точки А. Відповідно точка В (x0; у0) належить графіку функції у = cos х (рис. 2). Якщо точка А знаходиться правіше осі Оу, то косинус буде позитивний, якщо ж лівіше - негативний. Але в будь-якому випадку точка А не може покинути коло. Тому косинус лежить в межах від -1 до 1:
-1 = cos x = 1.
Додатковий поворот на будь-який кут, кратний 2 p. повертає точку A на те саме місце. Тому функція у = cos x періодична, її період дорівнює 2 p:
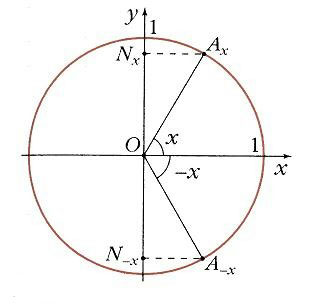
Якщо взяти два значення аргументу, рівні по абсолютній величині, але протилежні за знаком, x і -x, знайти на окружності відповідні точки Ax і А-x. Як видно на рис. 3 їх проекцією на вісь Ох є одна і та ж точка М. Тому
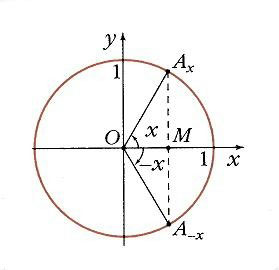
тобто косинус - парна функція, f (-x) = f (x).
Значить, можна досліджувати властивості функції y = cos х на відрізку [0, p], а потім врахувати її парність і періодичність.
При х = 0 точка А лежить на осі Ох, її абсциса дорівнює 1, а тому cos 0 = 1. Зі збільшенням х точка А пересувається по колу вгору і вліво, її проекція, природно, тільки вліво, і при х = p / 2 косинус стає дорівнює 0. Точка A в цей момент піднімається на максимальну висоту, а потім продовжує рухатися вліво, але вже знижуючись. Її абсциса все убуває, поки не досягне найменшого значення, рівного -1 при х = p. Таким чином, на відрізку [0, p] функція у = cos х монотонно убуває від 1 до -1 (рис. 4, 5).
З парності косинуса випливає, що на відрізку [- p. 0] функція монотонно зростає від -1 до 1, приймаючи нульове значення при х = - p / 2. Якщо взяти кілька періодів, вийде хвилеподібна крива (рис. 6).
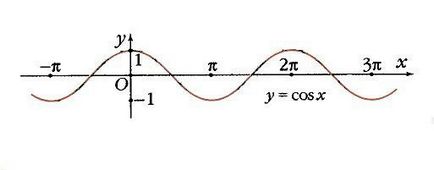
Отже, функція y = cos x набуває нульових значень в точках х = p / 2 + k p, де k - будь-яке ціле число. Максимуми, що дорівнюють 1, досягаються в точках х = 2k p. тобто з кроком 2 p. а мінімуми, рівні -1, в точках х = p + 2k p.
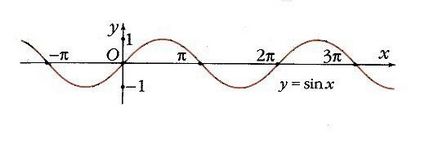
Функція y = sin х.
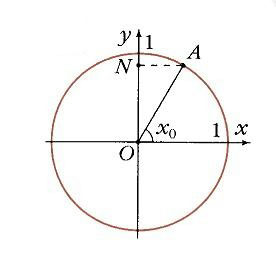
На одиничному колі кутку x0 відповідає точка А (рис. 7), а її проекцією на вісь Оу буде точка N. З начение функції у0 = sin x0 визначається як ордината точки А. Точка В (кут x0, у0) належить графіку функції y = sin x (рис. 8). Ясно, що функція y = sin x періодична, її період дорівнює 2 p:
Для двох значень аргументу, х і -, проекції відповідних їм точок Аx і Аx на вісь Оу розташовані симетрично відносно точки О. Тому
тобто синус - функція непарна, f (-x) = -f (x) (рис. 9).
Якщо точку A повернути щодо точки О на кут p / 2 проти годинникової стрілки (іншими словами, якщо кут х збільшити на p / 2), то її ордината в новому положенні буде дорівнює абсциссе в старому. А значить,
Інакше, синус - це косинус, «запізнілий» на p / 2, оскільки будь-яке значення косинуса «повториться» в синусі, коли аргумент зросте на p / 2. І щоб побудувати графік синуса, досить зрушити графік косинуса на p / 2 вправо (рис. 10). Надзвичайно важлива властивість синуса виражається рівністю