Складний рух точки приклади розв'язання задач
Розглянуто приклади розв'язання задач зі складним рухом точки. Точка рухається по прямій вздовж пластини. Пластина обертається навколо нерухомої осі. Визначається абсолютна швидкість і абсолютне прискорення точки.
Теорія, що застосовується для вирішення наведеної нижче завдання, викладається на сторінці "Складний рух точки, теорема Коріоліса".
Умова задачі
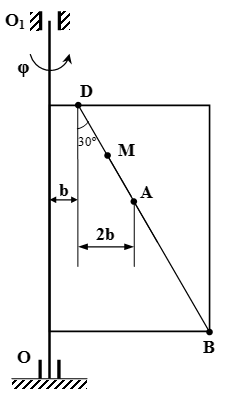
Малюнок до умові завдання
Прямокутна пластина обертається навколо нерухомої осі за законом φ = 6 t 2 - 3 t 3. Позитивний напрямок відліку кута φ показано на малюнках дугового стрілкою. Вісь обертання OO 1 лежить в площині пластини (пластина обертається в просторі).
За пластині уздовж прямої BD рухається точка M. Заданий закон її відносного руху, т. Е. Залежність s = AM = 40 (t - 2 t 3) - 40 (s - в сантиметрах, t - в секундах). Відстань b = 20 см. На малюнку точка M показана в положенні, при якому s = AM> 0 (при s <0 точка M находится по другую сторону от точки A ).
Знайти абсолютну швидкість і абсолютне прискорення точки M в момент часу t 1 = 1 с.
Вказівки. Це завдання - на складний рух точки. Для її вирішення необхідно скористатися теоремами про складання швидкостей і про складання прискорень (теорема Коріоліса). Перш ніж проводити всі розрахунки, слід за умовами завдання визначити, де знаходиться точка M на пластині в момент часу t 1 = 1 с. і зобразити точку саме в цьому положенні (а не в довільному, показаному на малюнку до задачі).
Рішення завдання
Дано: b = 20 см. Φ = 6 t 2 - 3 t 3. s = | AM | = 40 (t - 2 t 3) - 40. t 1 = 1 c.
Визначення положення точки
Визначаємо положення точки в момент часу t = t 1 = 1 c.
s = 40 (t 1 - 2 t 1 3) - 40 = 40 (1 - 2 · 1 3) - 40 = -80 см.
оскільки s <0. то точка M ближе к точке B, чем к D.
| AM | = | -80 | = 80 см.
Робимо малюнок.
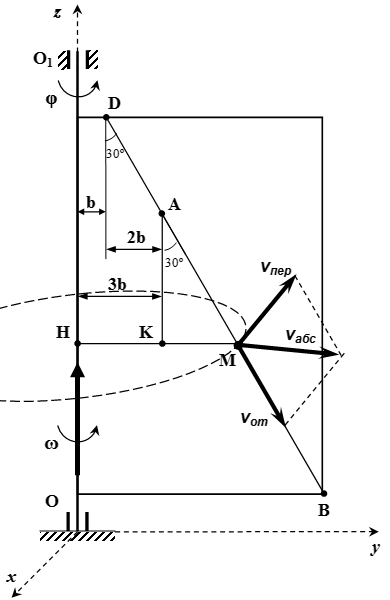
Відносна, переносна і абсолютна швидкість точки M
Визначення абсолютної швидкості точки
Згідно з теоремою про складання швидкостей. абсолютна швидкість точки дорівнює векторній сумі відносної і переносної швидкостей:
.
Визначення відносної швидкості точки
Визначаємо відносну швидкість. Для цього вважаємо, що пластина нерухома, а точка M здійснює заданий рух. Тобто точка M рухається по прямій BD. Диференціюючи s за часом t. знаходимо проекцію швидкості на напрям BD:
.
У момент часу t = t 1 = 1 с,
см / с.
Оскільки. то вектор направлений в напрямку, протилежному BD. Тобто від точки M до точки B. Модуль відносної швидкості
vот = 200 см / с.
Изображаем вектор на малюнку.
Визначення переносної швидкості точки
Визначаємо переносну швидкість. Для цього вважаємо, що точка M жорстко пов'язана з пластиною, а пластина робить заданий рух. Тобто пластина обертається навколо осі OO1. Диференціюючи φ за часом t. знаходимо кутову швидкість обертання пластини:
.
У момент часу t = t 1 = 1 с,
.
Оскільки. то вектор кутової швидкості спрямований в бік позитивного кута повороту φ. тобто від точки O до точки O1. Модуль кутовий швидкості:
ω = 3 с -1.
Изображаем вектор кутової швидкості пластини на малюнку.
З точки M опустимо перпендикуляр HM на вісь OO1.
При переносному русі точка M рухається по колу радіуса | HM | з центром в точці H.
| HM | = | HK | + | KM | = 3 b + | AM | sin 30 ° = 60 + 80 · 0,5 = 100 см;
Переносна швидкість:
vпер = ω | HM | = 3 · 100 = 300 см / с.
Вектор спрямований по дотичній до окружності в сторону обертання.
Визначення абсолютної швидкості точки
Визначаємо абсолютну швидкість. Абсолютна швидкість точки дорівнює векторній сумі відносної і переносної швидкостей:
.
Проводимо осі нерухомої системи координат Oxyz. Ось z направимо уздовж осі обертання пластини. Нехай в даний момент часу вісь x перпендикулярна пластині, вісь y лежить в площині пластини. Тоді вектор відносної швидкості лежить в площині yz. Вектор переносний швидкості спрямований протилежно осі x. Оскільки вектор перпендикулярний вектору. то по теоремі Піфагора, модуль абсолютної швидкості:
.
Визначення абсолютного прискорення точки
Згідно з теоремою про складання прискорень (теорема Коріоліса). абсолютне прискорення точки дорівнює векторній сумі відносного, переносного і коріолісова прискорень:
.
де
- кориолисово прискорення.
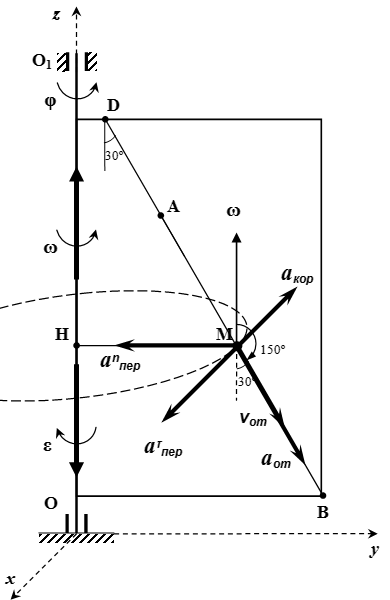
Відносне, переносне, кориолисово і абсолютне прискорення точки M
Визначення відносного прискорення
Визначаємо відносне прискорення. Для цього вважаємо, що пластина нерухома, а точка M здійснює заданий рух. Тобто точка M рухається по прямій BD. Двічі диференціюючи s за часом t. знаходимо проекцію прискорення на напрям BD:
.
У момент часу t = t 1 = 1 с,
см / с 2.
Оскільки. то вектор направлений в напрямку, протилежному BD. Тобто від точки M до точки B. Модуль відносного прискорення
aот = 480 см / с 2.
Изображаем вектор на малюнку.
Визначення переносного прискорення
Визначаємо переносне прискорення. При переносному русі точка M жорстко пов'язана з пластиною, тобто рухається по колу радіуса | HM | з центром в точці H. Розкладемо переносне прискорення на дотичне до кола та нормальне прискорення:
.
Двічі диференціюючи φ за часом t. знаходимо проекцію кутового прискорення пластини на вісь OO 1:
.
У момент часу t = t 1 = 1 с,
с -2.
Оскільки. то вектор кутового прискорення спрямований в бік, протилежний позитивного кута повороту φ. тобто від точки O1 до точки O. Модуль кутового прискорення:
ε = 6 с -2.
Изображаем вектор кутового прискорення пластини на малюнку.
Переносний дотичне прискорення:
a τ пер = ε | HM | = 6 · 100 = 600 см / с 2.
Вектор спрямований по дотичній до окружності. Оскільки вектор кутового прискорення спрямований в бік, протилежний позитивного кута повороту φ. то спрямований в бік, протилежний позитивному напрямку повороту φ. Тобто спрямований в бік осі x.
Переносний нормальне прискорення:
a n пер = ω 2 | HM | = 3 2 · 100 = 900 см / с 2.
Вектор спрямований до центру кола. Тобто в сторону, протилежну осі y.
Визначення коріолісова прискорення
Коріолісове (поворотний) прискорення:
.
Вектор кутової швидкості спрямований уздовж осі z. Вектор відносної швидкості спрямований уздовж прямої | DB |. Кут між цими векторами дорівнює 150 °. По властивості векторного добутку,
.
Напрямок вектора визначається за правилом свердлика. Якщо ручку свердлика повернути з положення в положення. то гвинт гвинта переміститься в напрямку, протилежному осі x.
Визначення абсолютного прискорення
Абсолютна прискорення:
.
Спроектуємо це векторне рівняння на осі xyz системи координат.
Модуль абсолютного прискорення: