Розподіл надлишкового заряду на провідниках в стані рівноваги

Головна | Про нас | Зворотній зв'язок
До провідникам відносяться речовини, які проводять електричний струм. У них є вільні заряди, які здатні переміщатися по провіднику під дією зовнішнього електричного поля. В металевих провідниках вільними зарядами є електрони, вони утворюють газ, що заповнює кристалічну решітку позитивно заряджених іонів.
Розглянемо, що станеться, якщо провіднику повідомити надлишковий заряд. При цьому позитивному заряду металевого провідника відповідає недолік вільних електронів, а негативному заряду - їх надлишок. В умовах рівноваги надлишкового заряду справедливі наступні твердження:
1.Електріческое поле всередині провідника відсутнє, а обсяг провідника і його поверхня є еквіпотенціальними
Дійсно, якщо рівності (2.39) не виконуються, то тоді вільні заряди в провіднику будуть переміщатися, так як робота сил електричного поля не дорівнюватиме нулю (). Це суперечить умові рівноваги надлишкового заряду: в умовах рівноваги вони повинні бути нерухомими.
2.Ізбиточний заряд розподіляється тільки по зовнішній поверхні провідника, так як через кулонівського відштовхування однойменних зарядів вони намагаються розійтися на максимально можливі відстані один від одного.
Це твердження можна довести, використовуючи теорему Гаусса. Виберемо всередині провідника довільну замкнуту поверхню (рис.3.14, а) і розрахуємо потік вектора через неї в умовах рівноваги. Врахуємо, що зв'язаних зарядів в металі не виникає (q '= 0) і тому з формули (3.27) слід
тобто всередині такої поверхні надлишкового заряду немає, так як цей заряд одного знака. Отже, він розташовується тільки на зовнішній поверхні провідника.
3.Распределеніе надлишкового заряду по зовнішній поверхні провідника є нерівномірним: модуль вектора і поверхнева щільність заряду # 963; більше в тих точках поверхні провідника, де її кривизна більше.
Кривизну поверхні в будь-якої її точки можна визначити радіусом R вписаною поблизу цієї точки сфери, а саме, кривизна поверхні обернено пропорційна R.
Доведемо Третє твердження. Для цього зазначимо, що висновки про електричному полі рівномірно зарядженої по поверхні сфери, зроблені в параграфі 3.1.8, справедливі і в разі зарядженої металевої сфери або кулі, так як кривизна поверхні у всіх її точках однакова, тобто надлишковий заряд розподіляється по ній рівномірно.
Якщо врахувати, що поверхня провідника можна представити у вигляді сукупності різних ділянок вписаних в неї сфер (рис.3.14, б) і використовувати формули (3.39) для Е і # 966; на поверхні сфери, то тоді можна записати:
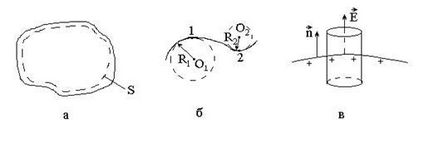
Відповідно до формули (3.42б) модуль вектора поблизу будь-якої точки поверхні зарядженого провідника пропорційний поверхневої густини заряду # 963; в цій точці. Формулу (3.42б) можна було отримати на основі теореми Гаусса, вибираючи допоміжну замкнуту поверхню у вигляді циліндра малого обсягу, що утворює якого перпендикулярна до поверхні провідника (рис.3.14, в). Вважаючи в межах циліндра електричне поле однорідним і застосовуючи формулу (3.29) прийдемо до вираження (3.42 б).
На рис. 3.15, а наведено графічне зображення за допомогою ліній електричного поля зарядженого провідника складної форми.
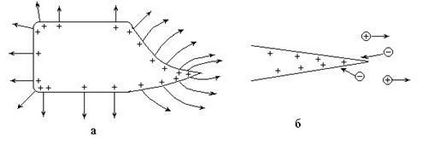
Потрібно врахувати, що лінії в усіх точках перпендикулярні до поверхні металу, так як вона є еквіпотенційної поверхнею.
Поблизу вістря модуль вектора може перевищити значення, відповідне іонізації молекул повітря (Еіоніз ≈3 × 10 6 В / м при атмосферному тиску), і тоді виникає явище стікання зарядів. що супроводжується електричним вітром.
Утворені при іонізації молекул електрони рухаються до вістря і компенсують на ньому частина заряду, рівновагу зарядів на провіднику порушується і до вістря підходять заряди з інших ділянок поверхні провідника (рис.3.15, б). Цей рух триває до тих пір, поки модуль напруженості електричного поля поблизу вістря буде перевищувати Еіоніз. В
Водночас позитивні іони молекул повітря рухаються в протилежному напрямку, від вістря, захоплюють за собою нейтральні молекули, створюючи руху повітря - електричний вітер.
Той факт, що надлишкові заряди в стані рівноваги знаходяться тільки на зовнішній поверхні провідника, дозволяє створити пристрої, здатні накопичувати великі заряди і досягати різниці потенціалів в кілька мільйонів вольт. До них можна віднести електростатичний генератор Ван-де-Грааф.
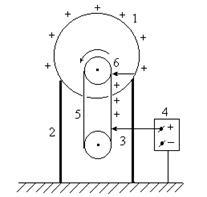
Він являє собою металеву сферу 1, закріплену на ізолюючої колоні 2 (рис. 3.16). На металеву щітку 3 поступаетположітельний заряд від джерела напруги 4 в кілька десятків кіловольт. Поблизу вістря щітки напруженість електричного поля перевищує Еіоніз молекул повітря (радіус вістря щітки r
1 мм, Е = 107 В / м) і заряд стікає на діелектричний транспортер 5 - рухому замкнуту стрічку з прогумованої тканини. Ця стрічка подає заряд всередину металевої сфери, він стікає на щітку і відразу надходить на зовнішню поверхню сфери. Максимально досяжна різниця потенціалів Uмакс в такому пристрої обмежується явищем стікання заряду з поверхні сфери, тобто виникненням розряду в повітрі при Есф≥Еіоніз. Величина Uмакс становить близько 10 мегавольт при радіусі сфери R = 5 м
Електричні генератори подібного типу використовуються головним чином в високовольтних прискорювачах заряджених частинок, а також в слаботочной високовольтної техніці.