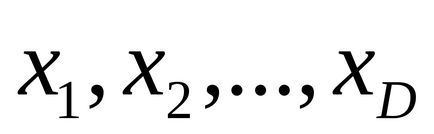Робота № 1

Попередня ◈ Наступна

Детермінізм - вчення про закономірності і причинної зумовленості всіх явищ природи і суспільства. В основі детермінованого опису (динамічного моделювання) лежить уявлення про те, що все майбутню поведінку об'єкта визначається його станом (x) в початковий момент часу. Станом (вектором стану) називають сукупність D величин:, гдеD - розмірність опису. величини

називаютсядінаміческімі змінними.

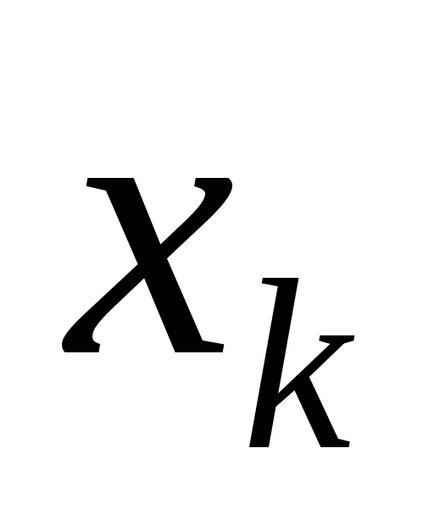
Правило, яким визначається еволюція об'єкта з плином часу, називають оператором еволюції. оператор еволюції

дозволяє за початковим станом

визначити стан об'єкта в будь-який інший час після цього часу

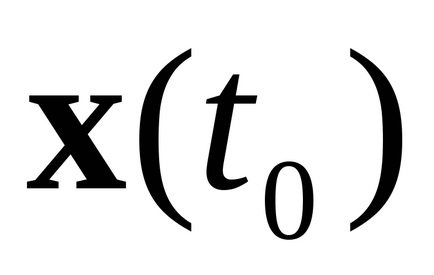
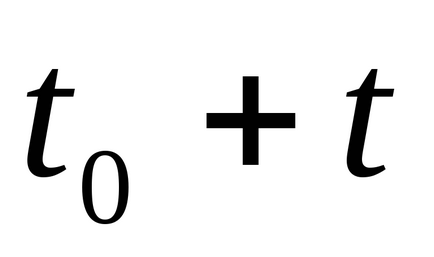
Математично оператор еволюції може бути заданий різними способами, що забезпечують виконання умови однозначності прогнозу. Класичним апаратом для завдання такого оператора є звичайні диференціальні рівняння (ОДУ). Теорема про існування та єдність їх рішення при заданих початкових умовах ( «даного справжньому відповідає одне майбутнє!») Забезпечило їм статус еталона для математичного опису явищ з позицій детермінізму.

Метою даної роботи є ілюстрація особливостей подання інформації за допомогою ОДУ.

Поле швидкостей.

ущественним гідністю динамічного моделювання є можливість наочного подання інформації, особливо у випадках малої розмірності сістемиD і малого числа параметрів. Для цього використовують формальні простору. простір станів (фазовий простір), пространствопараметров і різні їх гібридні варіанти. У цих випадках на осях координат формального простору відкладаються, відповідно, або значення динамічних змінних, або значення параметрів, або по одним - параметри, а за іншими - змінні.

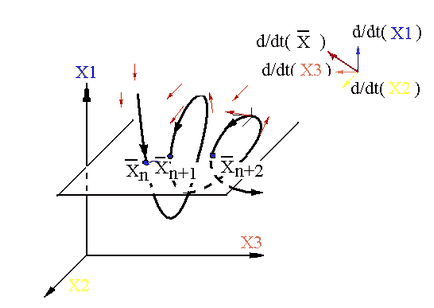
Станом x (t) в певний момент t в фазовому просторі відповідає точка з координатами -ізображающая точка (вона зображує миттєве стан). В процесі еволюції зображає точка з плином часу, зміщується вздовж деякої лінії - фазової траєкторії. Сукупність характерних фазових траєкторій називають фазовим портретом системи. При певному навику по фазового портрету можна Рис.1

багато сказати про можливі рухах системи.

При всьому різноманітті видів ОДУ найбільш популярною і має просте геометричне тлумачення є наступна форма запису:

До цієї форми можна привести будь-яку систему ОДУ, дозволену щодо старших похідних, навіть якщо вона містить явну залежність від часу. Систему (1) шляхом заміни змінних можна привести до виду:

де

- довільна гладка функція вектораx. , Наприклад,

. Форма (2) часто називаютстандартной. Ціною такого спрощення системи може бути збільшення її розмірності і складний вид єдиної функції в останньому рівнянні.

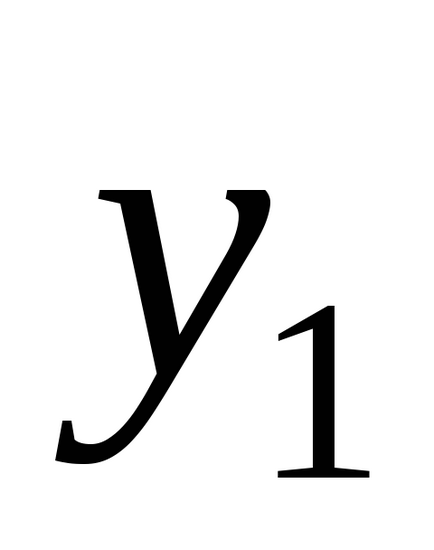
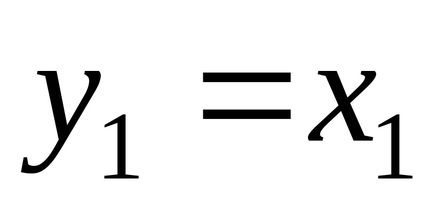
Геометричний сенс цього запису очевидний, якщо згадати, що стану - радіус-вектор в системі координат з відкладеними уздовж осей значеннями динамічних змінних, а тоді в лівій частині рівнянь записані проекції вектора швидкості ізмененіяx на осі

. Праві частини рівнянь вказують залежність цих проекцій від положення зображає точки в фазовому просторі. Іншими словами, система ОДУ (1) задає в кожній точці величину і напрямок вектора зміни стану (поля швидкостей). За вказаною вектором зміни стану напрямку зображає точка зміститься в фазовому просторі в наступний момент (рис.1). З плином часу точка буде описувати фазову траєкторію, при цьому вектор швидкості зміни стану в кожній точці спрямований по дотичній до неї.

Схожі статті

Попередня ◈ Наступна