рівносторонній п'ятикутник
Рівносторонній п'ятикутник часто зустрічається в структурі двоїстої пари ікосаедра і Додекаедр. При побудові даного багатокутника, зокрема, «від руки» - за допомогою циркуля і лінійки, часто виникає помітна похибка в розмірах його сторін. Наприклад, при розподілі окружності на п'ять рівних частин геометричним способом, або із застосуванням коефіцієнта (l = dk), хорди не завжди узгоджуються розмірами.
Кожен спосіб побудови рівностороннього п'ятикутника по - своєму унікальний. Найпростіше будувати n-косинці, якщо використовувати комп'ютер, наприклад, програмний додаток Corel DRAW. Слід лише відкрити меню об'єкт, вибрати інструмент багатокутник (п'ятикутник), клацнути і перетягнути курсор в потрібне місце - у вікно малювання, визначивши потрібний розмір фігури. Утримуванням натиснутою клавіші Ctrl отримують зображення рівностороннього багатокутника. Щоб задати число сторін або вершин при виборі багатокутника, то на відповідній панелі вводитися значення в поле число вершин або сторін багатокутника.
При створенні розгорток для тривимірного макетування, не виключаються різні способи n-вугільних фігур, в тому числі і спосіб «від руки». Для отримання рівностороннього п'ятикутника застосуємо метод динамічного прямокутника.
Правильний п'ятикутник закономірно розбивається власними діагоналями, побудова яких дають пентаграму - п'ятикутну зірку. Її центром є п'ятикутник. Його вершини - точки сторін пентаграми. Кожна точка ділить відповідну сторону п'ятикутної зірки на два пропорційних відрізка. Відомо, що ставлення довшого відрізка до меншого дорівнює приблизно 1. 618: 1, що прямо відноситься до «золотого перетину».
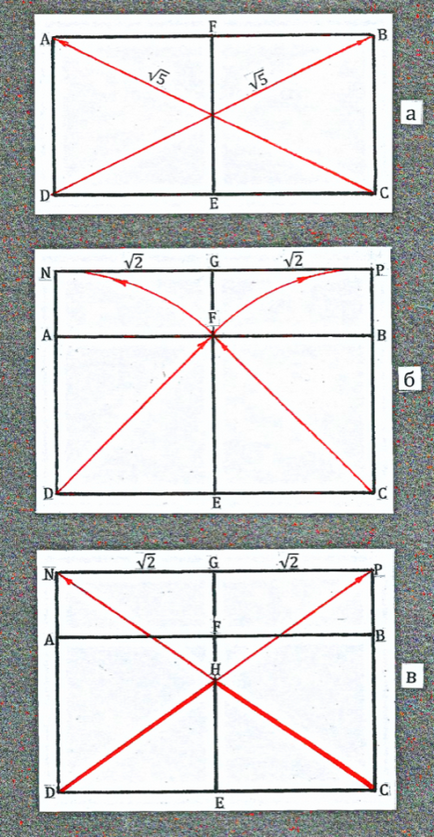
На малюнку 37а зображений прямокутник ABCD. Його складають два квадрата. Діагоналі рівні - гіпотенузи прямокутних трикутників.
На малюнку 37 б зображена схема побудови двох прямокутників на основі діагоналей DF і СF відповідних квадратів. Отримано пропорційний прямокутник NPCD.
Перетин діагоналей дають точку H - вершину споруджуваного п'ятикутника, а також дві його сторони HC, HD і його діагональ CD (рис. 37 в).
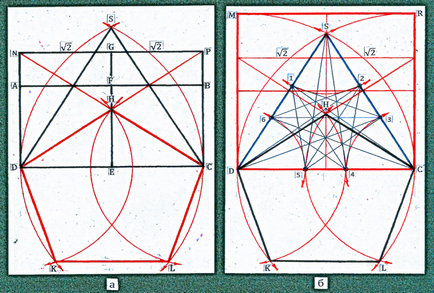
На малюнку 38а зображена схема побудови інших сторін п'ятикутника за допомогою перетину додаткових дуг з точок C і D як з центрів кіл.
На діагоналі CD (рис. 38б) дві дуги задають точки 4, 5. Вони ділять діагональ п'ятикутника відповідно до «золотими» пропорціями. На цій схемі виділені три фігури, що мають пряме відношення до дванадцятигранника - додекаедрів. Фігура HCLKD - його п'ятикутна грань, фігури MRCD і SCD - n -угольнікі, що обмежують малі діагональні площині перетину додекаедру. На площині рівностороннього трикутника SCD відображені сліди продовжень двоїстого ікосаедра.
Запропоновані схеми покрокового побудови правильного п'ятикутника призводять нас до реберно-сітчастим моделям двоїстої пари - ікосаедра і Додекаедр. На схемі (Додаток, рис. 80) представлений моночертёж. Тобто зображення багатокутних фігур, які обмежують діагональні площині перетину реберно-сітчастої моделі двоїстої пари правильних багатогранників.
Розуміння принципу продовження площин граней і способу побудови креслень (епюр), гарантують успішне оволодіння прийомами формоутворення, наприклад, зірчастих багатогранників. Кожна правильна (равногранного) і Напівправильні (неравногранний) багатогранники мають відповідно рівні утворюють ребра. На відміну від платонових, межі архімедівських тел, нерівні між собою. Їх межі, рівносторонній n-косинці, відрізняються своїми розмірами (рис. 1, фігури 10 - 23).
Відомо, що будь-які Платонова і архимедови багатогранники можна розмістити всередині сфери. Їх центри, отримані в результаті перетину осей симетрії, збігаються з центром сфери. Ця обставина важливо враховувати при визначенні розміру зірчастих багатогранників. Важливо і те, що розміри першої і наступних форм, отриманих продовженнями, будуть відрізнятися в бік їх збільшення. З методичної точки зору, в якості наочного матеріалу, корисно мати «ланцюжок» макетів, послідовно змінюються просторових форм.
На малюнку 39 моночертёж ікосаедра. На ньому відзначені вершини a, b, c, d, e, f, що збігаються з малою окружністю. Через них в тривимірному просторі проходять осі симетрії другого порядку.
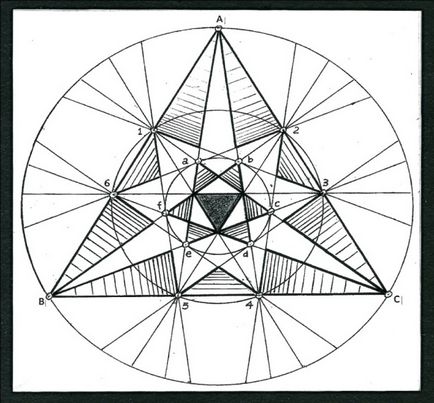
Плоскі фігури, заштриховані всередині кола, утворюють в тривимірному просторі чотиригранні кути. Вони об'єднуються в зірчасті форму - з'єднання п'яти октаедрів, рис. 40 (4).
Наступна середня окружність перетинає точки 1-6. Ці точки є вершинами відомих зірчастих багатогранників: третя, сьома і дев'ята форми ікосаедра (4). На малюнку 41 представлена Зірчаста форма під назвою «з'єднання десяти тетраедрів».


У центрі креслення (рис. 39) розташований рівносторонній трикутник - одна з двадцяти граней ікосаедра. До його сторонам примикають трикутник, які в тривимірному просторі об'єднуються в тригранні кути. Ці кути утворюють трикутні піраміди. Підстави пірамід збігаються з гранями багатогранника і складають першу зірчасті форму ікосаедра, рис. 42 (4).


Зовнішня велика окружність (рис. 39) перетинає точки A, B, C. Це вершини декількох зірчастих утворень, в яких збігаються межі зірчастої форми. Плоскі елементи, що утворюють опукло - увігнуту конструкцію десятігранного кута, заштриховані по всьому периметру рівностороннього трикутника ABC. Дванадцять таких конструкцій можна розташовувати, подібно «конструктору», на гранях додекаедру і закріплювати за допомогою клею. В результаті такого оформлення сформується Зірчаста форма великого ікосаедра (4). Цю форму пов'язують з іменами Кеплера-Пуансо (рис. 43).
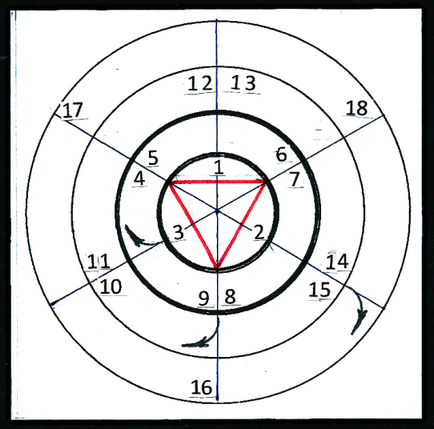
Щоб витягти з моночертежа необхідні конструктивні елементи тривимірних утворень, можна попередньо на макеті багатогранника пронумерувати межі і відзначити їх на графічній схемі (графі) груп симетричних площин (рис. 44).
В сукупності такі наочні моделі дозволяють, в якій мірі, контролювати порядок продовжених площин граней на плоскому полі креслення і в просторі. Включаючи в цей процес реберно-сітчасті моделі, можливо значно успішніше освоювати структуру тривимірного продовження.
У процесі створення розгорток відпадає необхідність здійснювати розрахунки параметрів плоских елементів (n-вугільних відсіків) на поле моночертежа. Його двомірна проекція містить натуральну метричну інформацію плоских геометричних фігур. Сліди різноспрямованих продовжених площин багатогранника перетинаються між собою на площині креслення. Іноді равнограннік називають ядром.
Розглянемо симетричні групи площин ікосаедра. На графі (рис. 44) зазначено номери граней. У центрі графа розташований рівносторонній трикутник - умовна грань
ікосаедра. Діаметрально протилежна паралельна їй грань на схемі не зображено. Два кола, навколо центрального трикутника, показані суцільними товстими лініями. Вони обмежують номера видимих граней на макеті ікосаедра, якщо дивитися на нього зверху з боку межі. Третя і четверта окружності обмежують номера невидимих граней. Вони зображені тонкими лініями. Осі симетрії проходять через вершини і серединні точки на сторонах трикутника. За номерами, що відносяться до тієї чи іншої окружності, визначається число граней (площин), що входять до відповідної симетричну групу.
Перша група - номера 1.2.3; друга група - 4.5.6.7. 8. 9; третя група - 10.11.12.13.14.15; четверта група - 16.17.18. Стрілки вказують перехід з однієї окружності на іншу.
Число площин симетричною групи співвідноситься з числом слідів на двомірному поле моночертежа. Слідами площин першої симетричною групи є відрізки 1.4; 2.5; 3.6. Сліди площин другий симетричній групи - відрізки 1.3; 3.5; 1.5; 2.6; 2.4; 4.6. Сліди площин третьою симетричною групи - відрізки A4; A5; B2; B3; З 1; C6. Сліди площин четвертої симетричною групи - відрізки AC; BC; AB (рис.39).
Процес продовження граней багатогранників призводить до різноманіття просторових форм. Цій темі було приділено велику увагу дослідниками (4, с.228, 229). Стали доступними результати математичних відкриттів в області класифікації багатогранних тел. Особливе місце займають зірчасті багатогранники.
Створюючи макети зірчастих структур, студенти часто стикаються з задовольняють результатами щодо точного побудови моночертежа. Креслення є відображенням площині, на якій всі інші площини продовжених граней багатогранника, залишаються слідами.
Роблячи акцент на січних площинах багатогранних тел, можна підкреслити, що запропоновані нами реберно-сітчасті моделі відображають принцип рубки простору.
За допомогою графа (рис. 44) і його опису простежується розподіл вісімнадцяти слідів продовжених площин (рис. 45).
Розглянемо геометричний порядок побудови моночертежа, часто зображуваного на сторінках даного матеріалу. На малюнку 45 моночертёж з обмеженим продовженням слідів площин граней в межах великого трикутника ABC. Нагадаємо, що три його сторони - сліди однієї з чотирьох симетричних груп площин граней ікосаедра. Побудова зводиться до простим графічним операціями. Задається окружність вільним радіусом і діленням її на шість частин. Виділяється рівносторонній трикутник ABC по трьом точкам розподілу окружності. На стороні BC будуються два перпендикуляра - BD і CE, які проходять через вільні точки поділу кола. Через точку A трикутника проводиться горизонтальна пряма лінія. Замикаються боку, що утворюють прямокутник BDEC, в який вписаний трикутник ABC. Прямокутник розбивається сіткою, що складається з дванадцяти осередків. Порядок побудови сітки легко визначається на представленому кресленні.
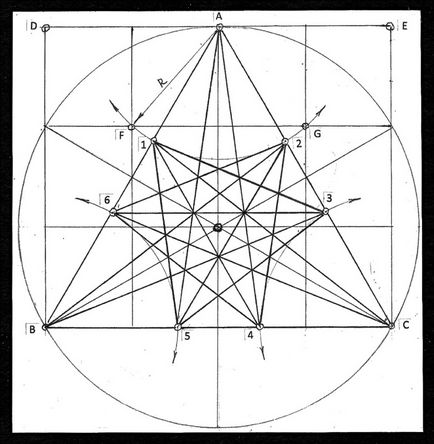
Через центр великого трикутника проводяться три бісектриси, які з'єднують вершини A, B, C з вільними точками ділення кола.
На даній стадії геометричної побудови всі крапки, необхідні для виконання горизонтальних і вертикальних ліній сітки, є на кресленні. Три сторони (сліди) трикутника ABC перетинаються з п'ятнадцятьма слідами інших трьох груп симетричних площин. Для цього на кожній стороні даного трикутника встановлюються по дві точки, кожна з яких ділить сторону щодо «золотого перетину». Наприклад, ставлення лінії AB (рис. 45) до відрізка A6 одно «золотим» пропорціям.
З точок A, B, C, як з центрів, радіусом AF або AG на сторонах великого трикутника засікаються шукані точки 1.6; 2.3; 3.4; 4.5. Встановлені точки на сторонах великого трикутника з'єднуються між собою відрізками прямих. Освіта двох рівносторонніх трикутників виходять з'єднанням між собою непарних (1. 3. 5), а потім парних (2. 4. 6) точок. Трьома парами прямих ліній з'єднуються вершинні точки A, B, C з точками, що лежать на протилежних сторонах трикутника. На кресленні прямі лінії проводяться паралельно сторонам AB, AC, BC, через пари точок 1.4; 2.5 і 3.6. В результаті нескладних геометричних побудов, виходить креслення, який називається «шаблон» (4) або «моночертеж» (2).
На малюнку 46 зображено креслення завершального продовження ікосаедра. Сліди його продовжених площин за межами зовнішньої окружності, не перетинаються, скільки б їх не продовжували. Кінцеві відсіки рубки простору площинами на моночертеже заштриховані. Вони вважаються завершальними і утворюють зірчасті форму ікосаедра (4, с.110).
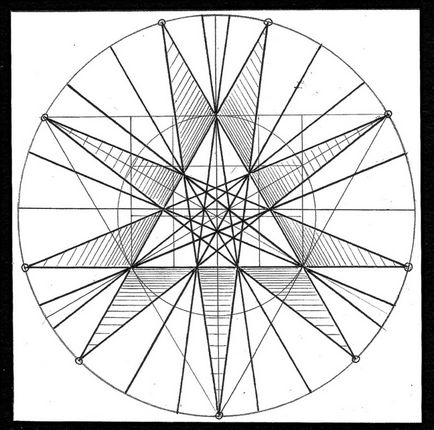
На зображенні відсутні позначення в порівнянні з попереднім малюнком 45. Креслення «в чистому» вигляді дозволяє сприймати плоскі елементи відсіків більш чітко. Це особливо важливо при тиражуванні n-кутників моночертежа. Спосіб перекаливанія їх голкою на заготовку в процесі макетування, дозволяє отримувати плоскі елементи для розгорток.
Щоб побудувати креслення завершального продовження ікосаедра, досить продовжити все лінії (сліди) за межі трикутника ABC до їх перетину (рис. 45). Зауважимо, що частина ліній будуть розходитися, а частина перетнуться між собою. За межами точок перетину все вісімнадцять ліній (слідів) будуть розходитися паралельними парами. Таке продовження слідів на кресленні (рис .45) не гарантує виключення похибки плоских фігур конструируемого макета.
Розглянемо малюнок 46. Для його побудови, як і раніше, використовується розподіл окружності на шість частин, а також прості прийоми геометричних побудов. За допомогою розчину циркуля, рівного радіусу кола, виконується такий спосіб розподілу.
Для поділу кола на будь-яке число рівних частин застосовується проста формула: l = dk. де l - довжина хорди, d - діаметр заданої окружності і k - коефіцієнт. Наприклад, для поділу кола на п'ять рівних частин коефіцієнт становить 0, 58779, а на шість - 0,50000 і т.д.
На малюнку 46 кінцеві вершини плоских елементів, завершального продовження, належать зовнішньому колу. Як і на попередньому малюнку 45 по точках поділу будується великий рівносторонній трикутник. Через центр кола і вершини трикутника проводяться бісектриси. Вони перетинаються з його сторонами і окружністю. Отримані точки на сторонах великого трикутника попарно з'єднуються прямими лініями, продовженими до перетину з зовнішньої окружністю. Через вершини малого рівностороннього трикутника проходить внутрішнє коло. На сторонах малого трикутника шикуються по дві точки на основі прямокутної сітки, способом, який був описаний (рис. 45). Ці точки можуть встановлюватися по-іншому. Для цього з'єднується кожна верхова точка великого трикутника з парами протилежних точок на великому колу, які дають продовжені боку малого трикутника. Побудовані таким способом лінії, перетинаються зі сторонами малого трикутника і утворюють шукані точки ділення.
Подальша побудова слідів продовжених площин виконується з урахуванням опису до малюнка 45.
Наведемо ще один спосіб як можна вибирати точки поділу сторін трикутника на кресленні ікосаедра. На зображенні (рис. 47) представлений креслення, точки поділу у якого, отримані методом прямокутного трикутника. По-перше, будується прямокутний трикутник з відносинами сторін 1: 2, і рівносторонній трикутник ABC.
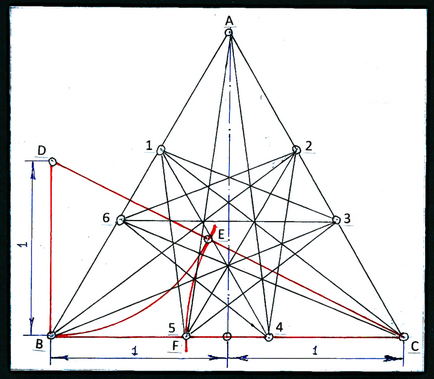
По-друге, проводиться дуга з точки D як з центру кола радіусом DB до перетину з гіпотенузою DC. По-третє, будується друга дуга з точки C радіусом CE до перетину з підставою трикутника. Точка F - точка поділу сторін рівностороннього трикутника. Відрізком BF з кожної вершини трикутника ABC встановлюються на його сторонах пари точок: 1.6; 2.3; і 4.5. Три сторони (AB, AC, CB) є слідами однієї з симетричних груп продовжених граней ікосаедра. П'ятнадцять слідів інших продовжень розподіляються на моночертеже відповідно до опису до малюнків 45, 46.