Рішення (перерахунок) симплекс-таблиці онлайн (правило прямокутника) (рішення задач з вищої

Розглянемо докладно, як проводиться перерахунок симплекс-таблиць (на прикладі однієї ітерації). Нехай є симплекс-таблиця представлена на Рис.1. Вирішується завдання максимізації цільової функції. Дозволяє стовпець відповідає змінної x2. а роздільна рядок змінної x3 (червоні числа), на їх перетині знаходиться дозволяє елемент (клітка з сірим фоном). Перше, що нам необхідно зробити - це замінити базисну змінну. Роздільна рядок показує, яка змінна повинна бути виведена з базису (в нашому випадку x3), а дозволяє стовпець показує яка змінна повинна увійти в базис (в нашому випадку x2). На Рис.2 факт заміни базисної змінної акцентований синьою лінією.
Тепер перерахуємо елементи стоять в роздільної рядку. Для цього просто розділимо кожен з них на дозволяючий елемент (в нашому прикладі 4). А все елементи дозволяє стовпця обнулив, крім елемента стоїть в роздільної рядку. (Дивись Рис.2)
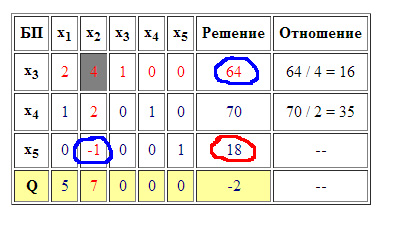
Інші елементи таблиці (крім стовпця "Відношення") перераховуються за так званим правилом прямокутника. сенс якого найпростіше зрозуміти на прикладі. Нехай потрібно перерахувати елемент обведений на Рис.1 червоним контуром. Подумки проводимо від нього вертикальну і горизонтальну лінії до перетину, з роздільною рядком і що дозволяє стовпцем. Елементи стоять в місцях перетину обведені синіми контурами (Дивись Рис.1). Нове значення "червоного" елемента дорівнюватиме нинішньому значенню елемента мінус твір "синіх" поділене на дозволяючий ( "сірий") елемент (Дивись Рис.1). Тобто. 18 - (64 * 1) / 4 = 34. який знаходиться поруч "*" показана операція множення.
Записуємо нове значення на колишнє місце (Дивись Рис.2 червоний контур).
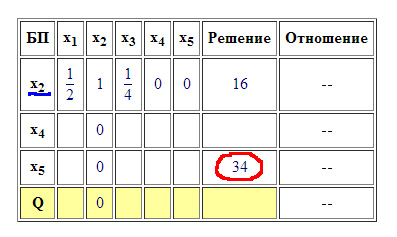
Користуючись цим правилом, заповнюємо всі порожні елементи таблиці (крім стовпця "Відношення") Дивись Рис.3. Після цього визначимо новий дозволяє стовпець. Для цього проаналізуємо рядок "Q" і так як наша задача на максимум, то знайдемо в ній максимальний позитивний елемент. він і визначить дозволяє стовпець. У нашому випадку це 3/2. Всі елементи дозволяє стовпця показані червоним шрифтом (Дивись Рис.3). Якщо після чергової ітерації в рядку "Q" не опиниться позитивних елементів - це значить що оптимальне рішення досягнуто, ітерації припиняються. Якби наша задача була на мінімум, то дозволяє стовпець визначався б за мінімальним негативного елементу, і якщо після чергової ітерації в рядку "Q" не опиниться негативних елементів, отже досягнуто оптимальне рішення.
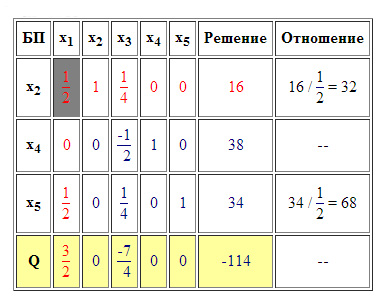
Тепер заповнимо стовпець "Відношення". Для цього потрібно відповідний (що стоїть в тому ж рядку) елемент стовпця "Рішення" розділити на відповідний елемент дозволяє стовпця (Дивись Рис.3). Зверніть увагу. що дана операція проводиться тільки для позитивних елементів дозволяє стовпця і рядок "Q" в даній операції не бере. Якщо після деякої ітерації в дозвільному стовпці не опиниться позитивних елементів, то дана задача нерозв'язна через необмеженість цільової функції, ітерації припиняються.
Після заповнення стовпця "Відношення" визначимо нову роздільну рядок. Вона визначається мінімальним елементом з шпальти "Відношення". У нашому випадку це 32. все елементи роздільної рядка показані червоним шрифтом (Дивись Рис.3). На цьому чергова ітерація закінчується, на наступній ітерації змінна x2 буде виведена з базису (про це нам говорить нова роздільна рядок), її місце займе змінна x1 (про це нам говорить новий дозволяє стовпець) і все обчислення повторяться знову.