Ренціал тичний і геометричний сенс диференціала

Діфференціалфункціі y = f (x) дорівнює добутку її похідної на приріст незалежної змінної x (аргументу) і обознвчается dy

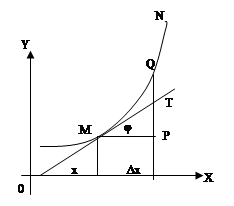
Диференціал функції, в загальному випадку відрізняючись від приросту функції, являє собою головну частину цього приросту, лінійну щодо збільшення аргумента.В цьому полягає аналітичний сенс диференціала

Диференціал функції є приростом ординати дотичної (АВ), яке відповідає збільшенню  х (МВ) абсциси. У цьому полягає геометричний зміст диференціала.

Диференціалом називають приріст аргументу, т.еdx = Δx

4.Первообразная функції. Невизначений інтеграл, його властивості. Таблиця основних невизначених інтегралів.

Функція F (x) називається первісною для функції f (x) на інтервалі (a, b), якщо вона диференційовна на цьому інтервалі і в кожній його точці

Безліч всіх первісних деякої функції f (x) називається невизначеним інтегралом функції f (x) і позначається як

Функція f (x) називається підінтегральної функцією, f (x) dx- подинтегрального виразом

Якщо F (x) - якась первісна функції f (x), то

де С - довільна стала.

Властивості неопр інтеграла:

Диференціал від невизначеного інтеграла дорівнює подинтегрального висловом

Похідна від невизначеного інтеграла дорівнює підінтегральної функції

Невизначений інтеграл від диференціала деякої функції дорівнює цій функції плюс довільна постійна

Постійний множник можна виносити за знак невизначеного інтеграла або вносити під знак інтеграла

Невизначений інтеграл від суми / різниці двох і більше функцій дорівнює сумі / різниці невизначених інтегралів від цих функцій

5. Визначений інтеграл. Формула Ньютона-Лейбніца. Властивості визначеного інтеграла. Геометричний сенс певного інтеграла. Визначений інтеграл.

Різниця F (b) -F (a) або значення приросту будь первообразной від даної функції f (x) при зміні аргументу від x = a до x = b називається певним інтегралом функції f (x) в межах від а до b.

це формула Ньютона-Лейбніца

Властивості визначеного інтеграла. 1. Визначений інтеграл з рівними межами дорівнює нулю: b∫af (x) dx = 0 2. При зміні місцями меж інтегрування величина певного інтеграла змінюється на протилежну: a∫bf (x) dx = -b∫af (x) dx 3 . Якщо відрізок інтегрування [a, b] розділений на кінцеве число nчастічних відрізків [a, x1], [x1, x2], .... [Xn-1, b], то визначений інтеграл від функції f (x) на відрізку [a, b] дорівнює сумі визначених інтегралів від цієї функції на кожному з часткових відрізків (властивостей аддитивности): a ∫ bf (x) dx = a ∫ x 1 f (x) dx + x1 ∫ x 2 + ...... .xn-1 ∫ bf (x) dx 4. a ∫ b kf (x) dx = ka ∫ bf (x) dx. де k- постійний множник 5. Визначений інтеграл від алгебраїчної суми кінцевого числа функцій, інтегрованих на відрізку [a, b], дорівнює алгебраїчній сумі визначених інтегралів цих функцій на даному відрізку. a ∫ b [f1 (x) + f2 (x) + .... + fn (x)] dx = a ∫ b f1 (x) dx + a ∫ b f2 (x) dx + ... ..a ∫ b fn ( x) dx Геометричний сенс певного інтеграла. Плоска фігура, обмежена зверху графіком неперервної функції y = f (x), знизу -осью абцісс, зліва-прямої лініейx = a, а праворуч - прямою лінією x = b, називається криволінійної трапецією. Площа криволінійної трапеції, обмеженою графіком функції y = f (x), восени абцісс і прямими лініями x = a і x = b, чисельно дорівнює визначеному інтегралу від цієї функції на відрізку [a, b]. В цьому і полягає геометрична інтерпретація.

6.Понятіе диференціального рівняння. Порядок рівняння, загальне і часткове рішення диференціального рівняння. Диференціальні рівняння першого порядку з відокремлюваними змінними, алгоритм їх решенія.Понятіе диференціального рівняння. Рівняння, в загальному випадку зв'язує шукану функцію y = f (x), її аргумент x, а також похідні різних порядків цієї функції. називається обикновеннимдіфференціальним рівнянням. F (x, y, y ', y' ', ......, y (n)) = 0 Порядок рівняння, загальне і часткове рішення диференціального рівняння. Порядкомдіфференціального рівняння називається порядок найвищої похідної, що входить в це рівняння.

Загальний вигляд диференціального рівняння першого порядку. F (x, y, y ') = 0Общім рішенням диференціального рівняння називається функція. задовольняє двом умовам: по-перше, ця функція повинна задовольняти даним диференціальних рівнянь, тобто при підстановці в рівняння повинна звертати його в тотожність; по-друге, кількість довільних постійних в цій функції має бути рівним порядку даного рівняння.

Загальна рішення диференціального рівняння n-го порядку має вигляд. y = F (x, C1, C2, ..., Cn)

Загальне рішення диференціального рівняння 1_ого порядку має вигляд. y = F (x, С)

На відміну від загального рішення диференціального рівняння його приватним рішенням називають будь-яку функцію, що задовольняє даному рівнянню, але не містить довільних постійних. Диференціальні рівняння першого порядку з відокремлюваними змінними, алгоритм їх вирішення.

Рівняння з відокремлюваними змінними має вид ___________________, причому його права частина може бути представлена ​​у вигляді добутку двох окремих функцій: _______________________________________________________________ .Тоді:

Можна перетворити це рівняння, розділивши змінні справа і зліва;

Загальний вигляд рівняння з розділеними змінними:

Рівняння вирішується безпосереднім інтегруванням: зліва по змінної y і праворуч по змінної х з додатком постійної С.

Вирішуючи це рівняння знайдемо відповідь: