Про математичних методах теорії надійності, резервування, резервні системи, булірованіе,
Про математичних методах теорії надійності
Для розвитку сучасної техніки і економіки, а також багатьох областей науки характерна не тільки автоматизація окремих операцій і цілих виробничих процесів, а й автоматизація самих процесів управління. Апаратура, яка використовується для цієї мети, ускладнюється з кожним роком, в зв'язку з тим що на неї покладається рішення все більш і більш відповідальних завдань. Потрібно визнати, що без такого ускладнення були б неможливі багато вражаючі досягнення останніх років. Так, без складних систем дистанційного керування було б немислимо налагодити експлуатацію атомних електростанцій або здійснити такі небувалі операції, як фотографування зворотного боку Місяця. А які колосальні і складні обчислення виробляють швидкодіючі електронні машини! Але тут виникає проблема: чим складніше такі вузли знаходяться, тим вище пред'являються до їх надійності вимоги, т. Е. До їх здатності протягом тривалого часу безвідмовно виконувати свої функції.
Дійсно, неважко уявити собі, що станеться, якщо відмовить система управління на атомній електростанції або в автоблокування на залізниці, на великій енергосистемі або на хімічному заводі.

Але не тільки для виробництва або запуску космічних кораблів потрібна висока надійність апаратури. Літаки повинні літати без аварій і слухняно виконувати волю пілота, автомобілі - безвідмовно перевозити вантажі та пасажирів, верстати - обробляти вироби із заданою точністю, штучне серце або штучні нирки - бездоганно виконувати свої функції під час складних операцій.
Особливо високі вимоги до надійності тієї апаратури, яку важко або неможливо виправити. А такої апаратури тепер в розпорядженні людства вже багато і буде все більше.
Щоб уявити собі складність сучасної апаратури, звернемося до прикладу, не вдаючись у технічні деталі. Сучасна електронна машина, яка виробляє величезні обчислювальні роботи, вирішальна логічні задачі (наприклад, переклад з однієї мови на іншу), що управляє виробничими процесами, зібрана з багатьох тисяч діодів, тріодів, конденсаторів, опорів, елементів пам'яті (феритових кілець), що підводять і ін . Кожен зі складових елементів не абсолютно надійний, т. е. є ймовірність виходу його з ладу в будь-який проміжок часу. Щоб таке складне устаткування діяло, необхідно кожен елемент підтримувати в робочому стані.
Ось чому так важливо заздалегідь, ще до початку роботи механізму, навчитися розраховувати його надійність, а також вибирати з різних варіантів конструкції ту, яка буде володіти найбільшою надійністю при збереженні інших необхідних якостей. У цих розрахунках обійтися без математичних методів неможливо, і тому в теорії надійності математика займає значне місце.
Перше завдання, яке доводиться вирішувати в теорії надійності, полягає в наступному: апаратура, як правило, виходить з ладу через псування будь-якого становить її елемента. Скільки часу проходить від початку його роботи до його псування? На це питання не може бути однозначної відповіді. Численні спостереження і спеціальні випробування показали, що навіть у виробів, виготовлених одночасно, час служби далеко не однаково. Взятий навмання з продукції, виготовленої одним робочим за зміну, напівпровідниковий діод або конденсатор може пропрацювати і кілька десятків тисяч годин, і тільки якусь сотню годин. Мова може йти не про точне передбачення числа годин, яка пропрацює деталь, а лише про ймовірність F (t) того, що вона пропрацює не менш t одиниць часу. Хоча для різних деталей ця ймовірність різна, все ж є і деякі загальні риси їхньої поведінки. Перш за все, на початку роботи (так званий період підробітки) ймовірність виходу з робочого стану підвищена; далі настає більш-менш тривалий період стабільності, коли ймовірність відмови за одиницю часу залишається незмінною; нарешті, настає період старіння, коли ймовірність псування швидко зростає.
Важливо відзначити, що якщо для окремих деталей закономірності розподілу відмов досить складні, то для складних систем, що складаються з великої кількості елементів і деталей, вдається вивести загальні і прості закономірності.
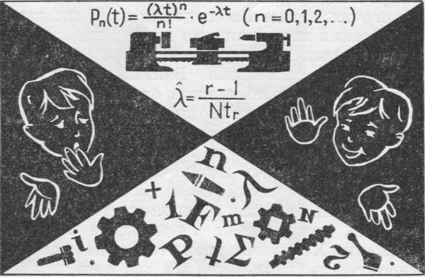
Припустимо, що кожен зіпсувався елемент негайно замінюється новим. Нехай нас цікавить апарат складається з дуже великого числа елементів, кожен з яких рідко виходить з робочого стану в порівнянні з відмовами хоча б одного з інших елементів, і відмови елементів незалежні один від одного. У цих припущеннях доводиться наступна важлива теорема: ймовірність того, що за проміжок часу t відбудеться п відмов, наближено дорівнює:
Перше завдання, яке доводиться вирішувати в теорії надійності, полягає в наступному: апаратура, як правило, виходить з ладу через псування будь-якого становить її елемента. Скільки часу проходить від початку його роботи до його псування? На цей
е 2,7182. а означає позитивне число, яке залежить від t. Фізичний сенс числа простий - це середнє число відмов системи в одиницю часу.
Щоб мати можливість заздалегідь розрахувати надійність виробу, потрібно знати надійність тих елементів, з яких воно буде виготовлено. З цією метою на заводах
влаштовують випробування і за їх результатами роблять висновок про якість елементів. Вибір тих величин, які повинні бути оцінені на підставі випробувань, умови, в яких вони мають виробляти, а також точність, яку потрібно отримати, не можуть бути призначені довільно; вони повинні визначатися фізичними і технічними міркуваннями. В яких умовах доведеться працювати виробу, як довго воно буде знаходитися в тих иЛи інших умовах? Все це повинно бути задано або конструктором, або експлуатаційників. Завдання математика полягає у виробленні плану: скільки виробів потрібно відчувати, протягом якого терміну, чи слід відмовили вироби замінювати на нові чи ні? Далі, математик повинен на підставі випробувань виявити наявність зв'язків між величинами, які цікавлять практика. Математик повинен вказати і той метод, яким слід користуватися для обробки результатів спостережень, а також зробити висновки з цієї обробки.
Нехай, для прикладу, нам відомо, що функція F
li, де X - невід'ємна постійна. Потрібно оцінити невідому величину X на підставі випробувань. З цим завданням доводиться часто зустрічатися в реальній обстановці, оскільки до цієї функції неминуче призводить той загальний результат, який був сформульований в теоремі про відмови складної апаратури.
Серед багатьох планів випробувань на надійність, запропонованих до теперішнього часу, ми вкажемо лише один: на випробування ставиться N однакових виробів, що відмовила виріб негайно замінюється новим, випробування проводяться до отримання г відмов (наприклад, г = 5 або 8). Які величини необхідно заміряти для можливо кращої оцінки невідомого X. Математична статистика вчить, що для цієї мети досить виміряти лише момент настання г-го відмови. Якщо він стався в момент tr, то найкращою оцінкою для X буде число:
Якщо ж ми відзначимо додатково момент першого, другого і наступних по порядку відмов (t \
У природі немає абсолютно надійних елементів і виробів. Кожен елемент, як би досконалий він не був, з часом втрачає свої властивості. Отримання елементів надвисокої надійності часто або взагалі недоступно існуючого рівня техніки, або вимагає таких великих витрат, що вони вже не можуть бути виправдані. Доводиться для підвищення надійності виробів йти іншими шляхами. Один з найпоширеніших шляхів підвищення надійності - шлях резервування. Сутність резервування полягає в тому, що в систему вводяться надлишкові елементи, вузли і навіть цілі агрегати, які включаються в роботу в міру виходу з робочого стану основних елементів (вузлів, агрегатів).
Так, на залізничних станціях стоять резервні тепловози, готові в будь-який момент змінити несправний рейсовий тепловоз; на великих аеродромах є резервні літаки; на великих електростанціях - резервні генератори: вони не дають струму в мережу, але в будь-який момент можуть замінити вибув з ладу генератор. Одна з елементарних завдань, яку ми зможемо негайно вирішити, полягає в наступному. У системі є елементи певного типу; в роботі повинно постійно знаходиться п елементів. Як зміниться надійність пристрою, якщо, крім п основних елементів, в навантаженому резерві (т. Е. В такому ж стані, в якому знаходяться працюючі елементи) знаходиться ще т елементів?
Якщо через р позначити ймовірність того, що даний елемент не вийде з робочого стану протягом необхідного нам часу, то ймовірність того, що жоден з п елементів за цей термін не вийде з ладу, по теоремі множення ймовірностей дорівнює р ". Це ймовірність безвідмовної роботи системи елементів, якщо відсутні резервні елементи. Нехай тепер в системі є т резервних елементів. в силу теореми додавання ймовірностей ймовірність того, що протягом часу t в системі буде зберігатися не менше п справних елементів, дорівнює:
Цей вислів - короткий запис суми | т + 1 доданків. Кожне з них записано під знаком замість i потрібно послідовно підставляти числа натурального ряду від 0 до т включно.
Розглянемо простий схематичний числовий приклад. Нехай п = 4, т = 1, р = 0,9. Неважко підрахувати, що ймовірність безвідмовної роботи системи без резерву дорівнює 0,6561, а при одному резервному елементі стає рівною 0,9185. Якби наша система мала не один, а два резервних елемента, то ймовірність її безвідмовної роботи піднялася б до 0,9841. Ми бачимо, що навіть невелике число резервних елементів різко збільшує надійність системи. Ось чому тільки один резервний генератор на електростанції майже повністю виключає можливість різкого зменшення вироблення електроенергії.

Завдання про резервування стає більш складною і цікавою, коли враховується додаткове обставина - відновлення поламаних елементів. Насправді у багатьох випадках, як тільки елемент виходить з робочого стану, його негайно починають ремонтувати.
Серед безлічі питань, пов'язаних з резервуванням, відзначимо зараз тільки один: скільки елементів необхідно мати в резерві, щоб домогтися заданої надійності системи? Це питання виникає постійно в найрізноманітніших областях техніки. Дійсно, для впевненої експлуатації системи управління потрібно знати, які її вузли необхідно зарезервувати і скільки кожного з них має бути в резерві. Подібні ж завдання виникають і при розрахунку резерву генераторів на електростанції, і при оснащенні космічних кораблів, що несуть в космос дослідників і прилади.
Як ми говорили, резервування вимагає введення в систему надлишкових елементів, а значить, збільшує її обсяг, вартість і ускладнює її. Всі ці моменти дуже серйозні, особливо для апаратури літаків, космічних кораблів, для приладів, які призначені для імплантації в організм (наприклад, стимулятори серцевої діяльності), для апаратів, які використовуються в післяопераційний період, слухових апаратів та ін. В такого роду апаратурі необхідно економити буквально кожен грам ваги і кожен сантиметр об'єму. У зв'язку з цим виникає нова цікава задача: знайти таке резервування, при якому система виявляється мак симально надійної, і при цьому вага апаратури, її обсяг і вартість не повинні перевищувати заданих розмірів. Так, для прикладу

Математична особливість поставленого завдання в тому, що ми шукаємо рішення серед цілих позитивних чисел п При конструюванні нових виробів і при розрахунку можливих поліпшень колишніх виключно важливо знати, який вплив на загальну надійність системи надає той чи інший елемент, той чи інший блок. Це знання дозволяє впевнено направляти дослідження на пошуки нових, більш надійних елементів. Але які елементи необхідно в першу чергу покращувати? Очевидно, ті, які максимально покращують надійність системи. Тут, як це не здається парадоксальним, може статися, що порівняно ненадійні елементи будуть надавати відносно мала вплив на надійність системи в цілому, і потрібно покращувати в першу чергу вже досить надійні елементи. Як це може бути? Дуже просто: може статися, що надійних елементів в системі багато, а менш надійних - лише одиниці.
Для пояснення цього твердження наведемо числовий приклад. Нехай в цікавій для нас системі є шість елементів першого типу і один елемент другого. Надійність елемента першого типу дорівнює 0,9, а другого - 0,8. Надійність всієї системи, в силу теореми множення ймовірностей, дорівнює 0,9б 0,8. Легко підрахувати, що збільшення надійності елемента другого типу на 10% збільшить надійність системи тільки на 10%. Збільшення ж надійності елемента першого типу тільки на 6% збільшить надійність системи майже на 40%
Цей невеликий підрахунок дуже повчальний і показує, як важливо інженеру, фізику і конструктору вміти користуватися математичним апаратом. Такий підрахунок може направити думку дослідника у вірному напрямку, може показати, де ховаються неполадки конструкції.
Ми торкнулися лише деякі питання нової науки - теорії надійності. Можливо, деяким з наших Новомосковсктелей доведеться в майбутньому впритул зайнятися за-1 дачами теорії надійності і розвивати її в різних напрямках, винаходити нові, | більш надійні елементи, створювати надійні схеми, розробляти методи дослідження і доводити нові загальні теореми цієї теорії.
Розміщення фотографій та цитування статей з нашого сайту на інших ресурсах дозволяється за умови вказівки посилання на першоджерело та фотографії.