Пряма і зворотна пропорційності
Якщо t - час рух пішохода (в годинах), s - пройдений шлях (в кілометрах), і він рухається рівномірно зі швидкістю 4 км / год, то залежність між цими величинами можна виразити формулою s = 4t. Оскільки кожному значенню t відповідає єдине значення s, то можна говорити про те, що за допомогою формули s = 4t задана функція. Її називають прямою пропорційністю і визначають наступним чином.
Визначення. Прямий пропорційністю називається функція, яка може бути задана за допомогою формули у = KХ, де k - нерівне нулю дійсне число.
Назва функції у = k х пов'язано з тим, що у формулі у = KХ є змінні х і у, які можуть бути значеннями величин. А якщо відношення двох величин дорівнює деякому числу, відмінному від нуля, їх називають прямо пропорційними. У нашому випадку = k (k ≠ 0). Це число називають коефіцієнтом пропорційності.
Функція у = k х є математичною моделлю багатьох реальних ситуацій, що розглядаються вже в початковому курсі математики. Одна з них описана вище. Інший приклад: якщо в одному пакеті борошна 2 кг, а куплено х таких пакетів, то всю масу купленої муки (позначимо її через у) можна представити у вигляді формули у = 2х, тобто залежність між кількістю пакетів і всією масою купленої муки є прямою пропорційністю з коефіцієнтом k = 2.
Нагадаємо деякі властивості прямої пропорційності, які вивчаються в шкільному курсі математики.
1. Областю визначення функції у = k х і областю її значень є безліч дійсних чисел.
2. Графіком прямої пропорційності є пряма, що проходить через початок координат. Тому для побудови графіка прямої пропорційності досить знайти лише одну точку, що належить йому і не збігається з початком координат, а потім через цю точку і початок координат провести пряму.
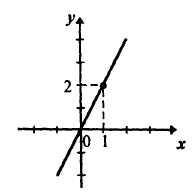
Наприклад, щоб побудувати графік функції у = 2х, досить мати точку з координатами (1, 2), а потім через неї і початок координат провести пряму (рис. 7).
3. При k> 0 функція у = KХ зростає на всій області визначення; при k <0 - убывает на всей области определения.
4. Якщо функція f - пряма пропорційність і (х1. У1), (х2. У2) - пари відповідних значень змінних х і у, причому х2 ≠ 0 то.
Дійсно, якщо функція f - пряма пропорційність, то вона може бути задана формулою у = KХ, і тоді в1 = kх1. у2 = kх2. Так як при х2 ≠ 0 і k ≠ 0, то у2 ≠ 0. Тому і виходить.
Якщо значеннями змінних х і у служать позитивні дійсні числа, то доведене властивість прямої пропорційності можна сформулювати так: зі збільшенням (зменшенням) значення змінної х в кілька разів відповідне значення змінної у збільшується (зменшується) у стільки ж разів.
Це властивість властива тільки прямий пропорційності, і їм можна користуватися при вирішенні текстових завдань, в яких розглядаються прямо пропорційні величини.
Завдання 1. За 8 год токар виготовив 16 деталей. Скільки годин буде потрібно токареві на виготовлення 48 деталей, якщо він буде працювати з тією ж продуктивністю?
Рішення. У задачі розглядаються величини - час роботи токаря, кількість зроблених ним деталей і продуктивність (тобто кількість деталей, що виготовляються токарем за 1 год), причому остання величина постійна, а дві інші приймають різні значення. Крім того кількість зроблених деталей і час роботи- величини прямо пропорційні, так як їх відношення дорівнює деякому числу, не рівній нулю, а саме - числу деталей, що виготовляються токарем за 1 год. Якщо кількість зроблених деталей позначити буквою у, час роботи х, а продуктивність - k, то отримаємо, що = k або у = KХ, тобто математичною моделлю ситуації, представленої в завданні, є пряма пропорційність.
Вирішити завдання можна двома арифметичними способами:
1 спосіб: 2 спосіб:
1) 16: 8 = 2 (дет.) 1) 48:16 = 3 (рази)
2) 48: 2 = 24 (ч) 2) 8-3 = 24 (ч)
Вирішуючи задачу першим способом, ми спочатку знайшли коефіцієнт пропорційності до, він дорівнює 2, а потім, знаючи, що у = 2х, знайшли значення х за умови, що у = 48.
При вирішенні задачі другим способом ми скористалися властивістю прямої пропорційності: у скільки разів збільшується кількість деталей, зроблених токарем, у стільки ж разів збільшується і кількість часу на їх виготовлення.
Перейдемо тепер до розгляду функції, званої зворотної пропорційністю.
Якщо t - час руху пішохода (в годинах), v - його швидкість (в км / год) і він пройшов 12 км, то залежність між цими величинами можна виразити формулою v # 8729; t = 20 або v =.
Оскільки кожному значенню t (t ≠ 0) відповідає єдине значення швидкості v, то можна говорити про те, що за допомогою формули v = задана функція. Її називають зворотної пропорційністю і визначають наступним чином.
Визначення. Зворотною пропорційністю називається функція, яка може бути задана за допомогою формули у =. де k - нерівне нулю дійсне число.
Назва даної функції пов'язано з тим, що в у = є змінні х і у, які можуть бути значеннями величин. А якщо твір двох величин дорівнює деякому числу, відмінному від нуля, то їх називають обернено пропорційними. У нашому випадку ху = k (до ≠ 0). Це число k називають коефіцієнтом пропорційності.
Функція у = є математичною моделлю багатьох реальних ситуацій, що розглядаються вже в початковому курсі математики. Одна з них описана перед визначенням зворотної пропорційності. Інший приклад: якщо купили 12 кг борошна і розклали її в л: банок по у кг в кожну, то залежність між даними величинами можна представити у вигляді х-у = 12, тобто вона є зворотною пропорційністю з коефіцієнтом k = 12.
Нагадаємо деякі властивості зворотної пропорційності, відомі зі шкільного курсу математики.
1.Область визначення функції у = і областю її значень х є безліч дійсних чисел, відмінних від нуля.
2. Графіком оберненої пропорційності є гіпербола.
3. При k> 0 гілки гіперболи розташовані в 1 -й і 3-й чвертях і функція у = є спадною на всій області визначення х (рис. 8).
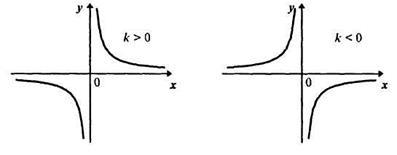
при до <0 ветви гиперболы расположены во 2-й и 4-й четвертях и функция у = является возрастающей на всей области определения х (рис. 9).
4. Якщо функція f - зворотна пропорційність і (х1. У1), (х2. У2) - пари відповідних значень змінних х і у, то.
Дійсно, якщо функція f - зворотна пропорційність, то вона може бути задана формулою у =, і тоді. Так як х1 ≠ 0, х2 ≠ 0, х3 ≠ 0, то
Якщо значеннями змінних х і у служать позитивні дійсні числа, то це властивість зворотної пропорційності можна сформулювати так: зі збільшенням (зменшенням) значення змінної х в кілька разів відповідне значення змінної у зменшується (збільшується) у стільки ж разів.
Це властивість властива тільки зворотної пропорційності, і їм можна користуватися при вирішенні текстових завдань, в яких розглядаються обернено пропорційні величини.
Завдання 2. Велосипедист, рухаючись зі швидкістю 10 км / год, проїхав відстань від А до В за 6 год. Скільки часу витратить велосипедист на зворотний шлях, якщо буде їхати зі швидкістю 20 км / год?
Рішення. У задачі розглядаються величини: швидкість руху велосипедиста, час руху і відстань від А до В, причому остання величина постійна, а дві інші приймають різні значення. Крім того, швидкість і час руху - величини обернено пропорційні, так як їх добуток дорівнює деякому числу, а саме пройденого відстані. Якщо час руху велосипедиста позначити буквою у, швидкість - х, а відстань АВ - k, то отримаємо, що ху = k або у =. тобто математичною моделлю ситуації, представленої в завданні, є зворотна пропорційність.
Вирішити завдання можна двома способами:
1 спосіб: 2 спосіб:
1) 10-6 = 60 (км) 1) 20:10 = 2 (рази)
2) 60:20 = 3 (4) 2) 6: 2 = 3 (ч)
Вирішуючи задачу першим способом, ми спочатку знайшли коефіцієнт пропорційності до, він дорівнює 60, а потім, знаючи, що у =. знайшли значення у за умови, що х = 20.
При вирішенні задачі другим способом ми скористалися властивістю зворотної пропорційності: у скільки разів збільшується швидкість руху, в стільки ж разів зменшується час на проходження одного і того ж відстані.
Зауважимо, що при вирішенні конкретних завдань з обернено пропорційними або прямо пропорційними величинами накладаються деякі обмеження на х і у, зокрема, вони можуть розглядатися не на всій множині дійсних чисел, а на його подмножествах.
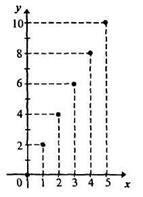
Завдання 3. Олена купила х олівців, а Катя в 2 рази більше. Позначте число олівців, куплених Катею через у, висловіть у через х і побудуйте графік встановленого відповідності за умови, що х≤5. Чи є це відповідність функцією? Яка її область визначення і область значень?
Рішення. Катя купила у = 2х олівців. При побудові графіка функції у = 2х необхідно врахувати, що змінна х позначає кількість олівців і х≤5, значить, вона може приймати тільки значення 0, 1, 2, 3, 4, 5. Це і буде область визначення даної функції. Щоб отримати область значень даної функції, треба кожне значення х з області визначення помножити на 2, тобто це буде безліч. Отже, графіком функції у = 2х з областю визначення буде безліч точок, зображених на малюнку 10. Всі ці точки належать прямій у = 2х.