потужність безлічі

Розглянемо безліч A і сукупність всіх множин, еквівалентних безлічі A. На підставі властивості транзитивності всі ці безлічі будуть еквівалентні між собою.

Назвемо таку сукупність множин класом еквівалентності.

Кожному класу еквівалентності поставимо у відповідність деякий символ  (альфа), який будемо називати кардинальним числом або потужністю кожного безлічі, що входить в даний клас еквівалентності.

Таким чином, під потужністю безлічі

розуміється щось спільне, що притаманне всім еквівалентним між собою безлічам.

Якщо заданий клас еквівалентних множин і цього класу множин поставлено у відповідність кардинальне число

, то,, ...,.

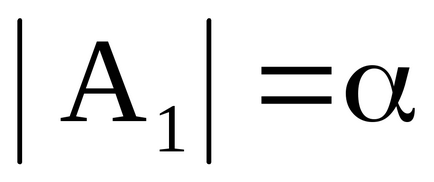
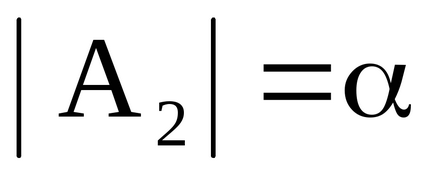
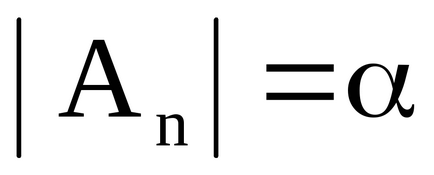
Для кінцевих множин поняття «число елементів» і поняття потужності множин збігаються між собою.

Для нескінченних множин поняття «число елементів» сенсу не має. Можна говорити тільки про потужність безлічі. Поняття потужності є природне узагальнення поняття числа елементів.

Нехай - множина натуральних чисел менших або рівних

.

Визначення. Кінцевим безліччю називається безліч, рівносильне безлічі

- натуральних чисел менших або рівних. воно міститьелементів і його потужність дорівнює. пишуть.

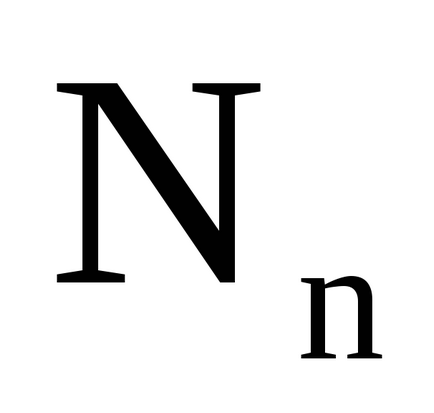
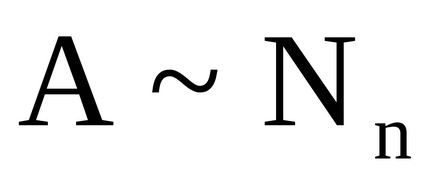
Потужність порожнього безлічі дорівнює нулю

.

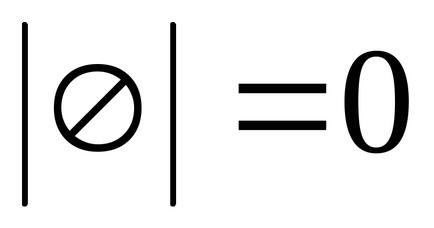
Визначення. Непорожнє і неконечную безліч називається нескінченним.

Теорема. Потужність безлічі A завжди строго менше потужності безлічі всіх його підмножин.

Визначення. Будь-яке підмножина рівносильне безлічі натуральних чисел називається рахунковим. і його потужність дорівнює

(Алеф нуль):

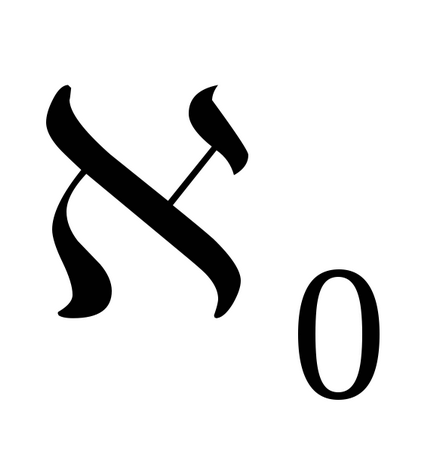
Зауваження. Алеф - перша буква єврейського алфавіту, а

- найменша потужність нескінченної кількості.

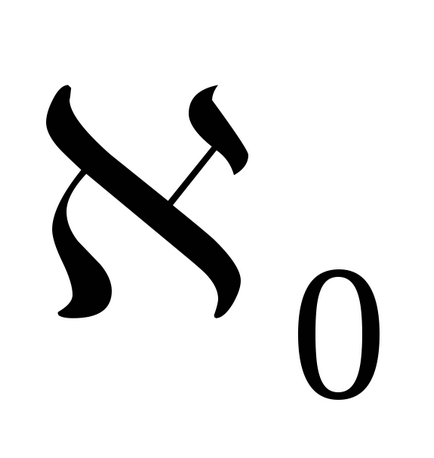
Теорема. Безліч всіх підмножин ℬ

безлічі натуральних чисел незліченно. Його потужність називається мощностьюконтінуума і дорівнює 1 (алеф один):

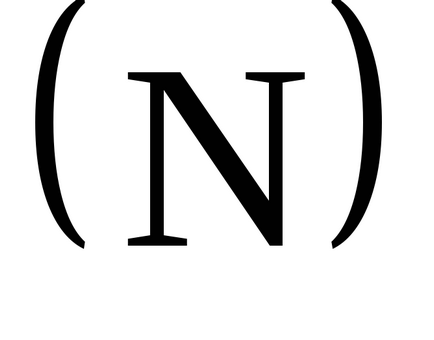
Приклад. Потужність безлічі дійсних чисел сегмента

дорівнює потужності континууму.

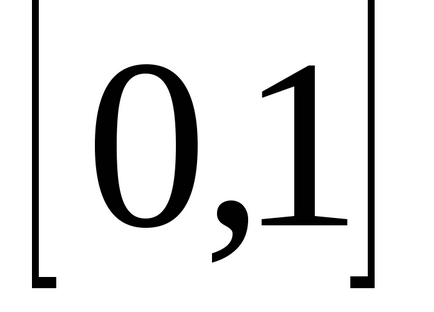
Теорема. Будь-яке безліч містить рахункове підмножина.

Доведення. Нехай A - безліч. Оскільки

, ми можемо вибрати серед його елементів якої-небудь один; нехай це буде, тоді безліч; виберемо в ньому будь-якої іншої елемент - наприклад,. Після виділення таким способомелементів безліч, і можна вибрати ще один елемент, наприклад,і т.д. Отже, безліч A містить рахункове підмножина.

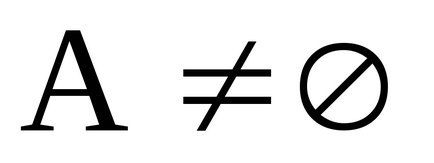
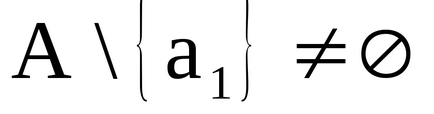
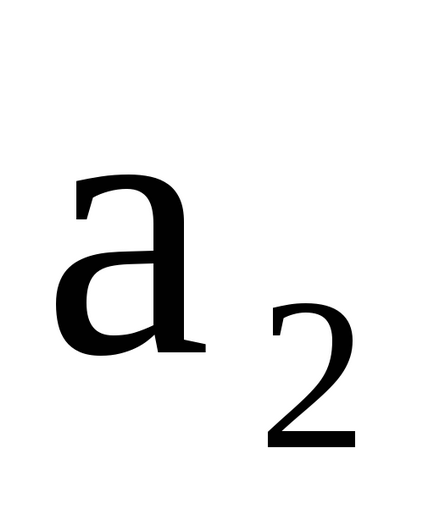
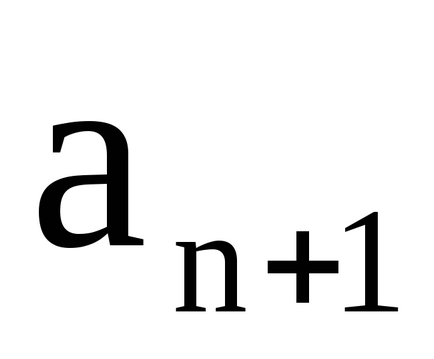
Теорема. Об'єднання безлічі континууму і кінцевого або рахункового безлічі має потужність континууму.

Теорема. Об'єднання кінцевого або рахункового числа множин потужності континууму має потужність континууму.

Характеристична функція підмножин.

Визначення. Характеристичної функцією підмножини

називається функція, певна на універсальній множині U наступним чином:

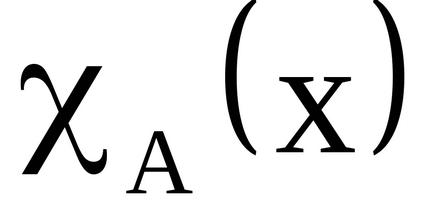
якщо

, то характеристична функція перетину двох підмножиндорівнює:

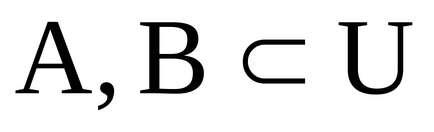
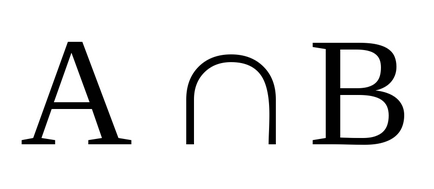
Характеристична функція доповнення безлічі

дорівнює:

Для отримання виразу для характеристичної функції об'єднання двох підмножин

скористаємося очевидним співвідношеннямі формулою де Моргана.

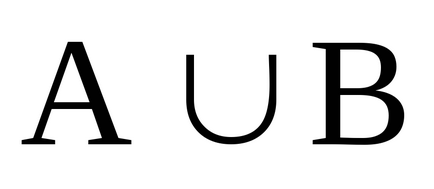
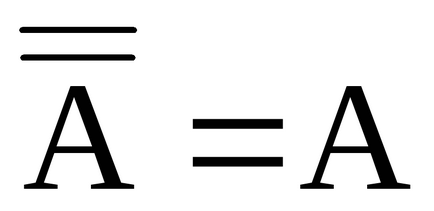
Для кінцевого безлічі A з визначення характеристичної функції випливає, що

Схожі статті

• Операції над множинами в delphi, delphi, компоненти delphi, вихідні коди delphi

• Адаптація до м'язової роботі максимальної і субмаксимальної потужності

• Вал відбору потужності, і його застосування