Побудова таблиць істинності
Пріоритетом у виконанні порядку виконання операцій користуються дужки.
Алгоритм побудови таблиці істинності логічної функції
Визначають кількість рядків: кількість рядків = $ 2 ^ n + 1 $ (для рядка заголовка). $ N $ - кількість простих виразів. Наприклад, для функцій двох змінних існує $ 2 ^ 2 = 4 $ комбінації наборів значень змінних, для функцій трьох змінних - $ 2 ^ 3 = 8 $ і т.д.
Визначають кількість стовпців: кількість стовпців = к-ть змінних + к-ть логічних операцій. При визначенні кількості логічних операцій враховують також порядок їх виконання.
Заповнюють стовпці результатами виконання логічних операцій в певній послідовності, враховуючи таблиці істинності основних логічних операцій.
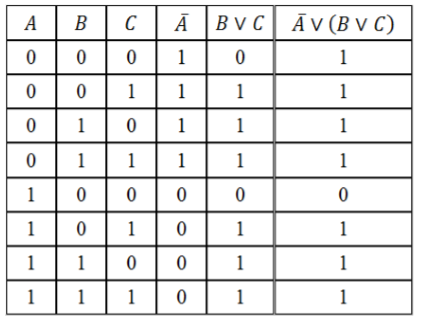
Скласти таблицю істинності логічного виразу $ D = \ bar \ vee (B \ vee C) $.
Визначимо кількість рядків:
Кількість простих виразів - $ n = 3 $, значить
кількість рядків = $ 2 ^ 3 + 1 = 9 $.
Визначимо кількість стовпців:
Кількість змінних - $ 3 $.
Кількість логічних операцій і їх послідовність:
- інверсія ($ \ bar $);
- диз'юнкція, тому що вона знаходиться в дужках ($ B \ vee C $);
диз'юнкція ($ \ overline \ vee \ left (B \ vee C \ right) $) - шукане логічне вираз.
Кількість стовпців = $ 3 + 3 = 6 $.
Заповнимо таблицю, враховуючи таблиці істинності логічних операцій.
Визначимо кількість рядків:
Кількість простих виразів - $ n = 3 $, значить
кількість рядків = $ 2 ^ 3 + 1 = 9 $.
Визначимо кількість стовпців:
Кількість змінних - $ 3 $.
Кількість логічних операцій і їх послідовність:
- заперечення ($ \ bar $);
- диз'юнкція, тому що вона знаходиться в дужках ($ A \ vee B $);
- кон'юнкція ($ (A \ vee B) \ bigwedge \ overline $);
- заперечення, яке позначимо $ F_1 $ ($ \ overline> $);
- диз'юнкція ($ A \ vee C $);
- кон'юнкція ($ (A \ vee C) \ bigwedge B $);
- заперечення, яке позначимо $ F_2 $ ($ \ overline $);
Кількість стовпців = $ 3 + 8 = 11 $.
Заповнимо таблицю, враховуючи таблицю істинності логічних операцій.
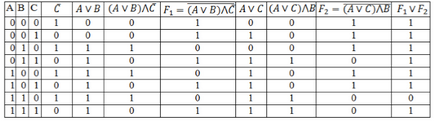
Алгоритм побудови логічної функції по її таблиці істинності
- Виділяють в таблиці істинності рядки зі значенням функції, рівним $ 1 $.
- Виписують шукану формулу як диз'юнкцію декількох логічних виразів. Кількість цих виразів дорівнює кількості виділених рядків.
- Кожне логічне вираз в цій диз'юнкції записати як кон'юнкцію аргументів функції.
- У разі, коли значення якогось із аргументів функції у відповідному рядку таблиці приймає значення $ 0 $, то цей аргумент записати у вигляді його заперечення.
Вирішуємо контрольні з усіх предметів. 10 років досвід! Ціна від 100 руб. термін від 1 дня!