Об'єднання множин, теорія множин, приклади рішень завдань
- Об'єднанням або сумою n множин A 1. A2. ..., An називається безліч. що складається з елементів. що входять хоча б в одне з цих n множин. A = A1 U A2 U ... U An де знак U позначає операцію об'єднання множин.
Формально операція об'єднання множин визначається наступним чином.
де ∨ - логічний знак. позначає союз АБО. Новомосковскется цей запис так. безліч А - це все ті значення х. які належать множині А1. або безлічі А2. або безлічі А3 і так далі до безлічі Ап.
Для виконання операції об'єднання множин є калькулятор операцій над множинами.
Наприклад. нехай дано безлічі. A1 =; A2 =; A3 =. Застосувавши до них операцію об'єднання. отримаємо нове безліч A = A1 U A2 U A3 =. Зауважимо. що b ∈ A1 і b ∈ A3. проте в безліч A елемент b входить тільки один раз (згадаємо. всі елементи множини повинні бути різними).
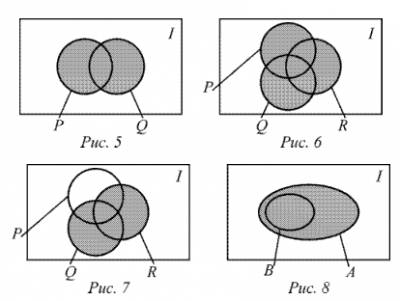
На діаграмах Венна (калькулятор) об'єднання множин позначають суцільною штрихуванням областей, які відповідають цим множинам:
- На рис. 5 заштрихована область безлічі Q U P,
- На рис. 6 показана штрихуванням область безлічі (P U Q) U R.
- На рис. 7 зображено три безлічі P, Q і R. Штрихуванням відзначено безліч Q U R.
Операція об'єднання множин має такі властивості:
а) об'єднання коммутативно:
A U B U C = A U C U B = B U A U C і т.д.;
б) об'єднання асоціативно:
(A U B) U C = A U (B U C) = A U B U C.
(Завдяки асоціативності при записі кількох множин. З'єднаних знаком об'єднання. Дужки можна не використовувати);
в) якщо B ⊆ A або B ⊂ A, то A U B = A.
На рис. 8 приведена діаграма Венна для випадку. коли B ⊂ A.
Штрихуванням відзначена область безлічі A, яка
одночасно відноситься і до безлічі A U B.
- З властивості «в» слід. що:
- A U A = A;
- A U A = ∅;
- A U I = I.
1. Знайдіть елементи безлічі A U B. якщо
2. Знайдіть елементи множин. спочатку A, потім - A1. після цього - A2 (числа впорядкувати по зростанню), якщо A = 1 ∨ x ∈ A2); A1 ⊂ I - безліч чисел. кратних трьом; A2 ⊂ I - безліч чисел. кратних чотирьом>; I =.
3. Дано три безлічі A, B, C. Відомо. що a ∈ A. Вкажіть всі вірні твердження.
а) a ⊂ B; е) ∈ B;
б) a ∈ A U B; ж) ⊆ A U B;
в) a ⊂ B U C; з) ∈ B U C;
г) a ∈ A U B U C; і) ⊆ A U B U C
Відповіді: б), г), д), ж), і) - істинно.
4. На рис. 9 приведена діаграма Венна для трьох множин. Знайдіть елементи множин A U B. потім - A U C.
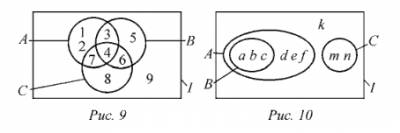
5. Перелічіть елементи безлічі M (рис. 9):
6. Перерахуйте елементи безлічі N (рис. 9):
7. Перерахуйте елементи безлічі K, якщо
8. Перелічіть елементи безлічі T (рис. 9):
9. Знайдіть кардинальне число безлічі A U B.
Відповідь: | A U B | = 7
10. Знайдіть кардинальні числа множин
A U B, A U C, B U C по діаграмі Венна (рис. 10).
11. Знайдіть кардинальне число безлічі A U B. якщо
Відповідь: | A U B | = 5
12. Знайдіть кардинальне число безлічі A U B. якщо A =; B =.
Відповідь: | A U B | = 4
13. Знайдіть кардинальне число безлічі B (P) U B (Q), де
Відповідь: | B (P) U B (Q) | = | B (P U Q) | = | B
14. Знайдіть кардинальне число безлічі B (K) U B (M), де
15. Скільки власних підмножин має безліч. A = A1 U A2 U ... U An.
якщо A1. A2, ..., An - Синглетон. попарно нерівні між собою.