Методичка 866 - глава 5
де x 1. x 2. .... xn - деякі параметри об'єкта оптимізації.
Існують два типи завдань оптимізації - безумовні і умовні.
Безумовна задача оптимізації полягає в знаходженні максимуму або мінімуму дійсної функції (5.1) від n дійсних змінних і визначенні відповідних значень аргументів.
Умовні задачі оптимізації. або завдання з обмеженнями, - це такі, при формулюванні яких на значення аргументів накладаються обмеження у вигляді рівності або нерівностей.
Рішення задач оптимізації, в яких критерій оптимальності є лінійною функцією незалежних змінних (тобто містить ці змінні в першого ступеня) з лінійними обмеженнями на них, становить предмет лінійного програмування.
Слово «програмування» відображає тут кінцеву мету дослідження - визначення оптимального плану або оптимальної програми, по якій з безлічі можливих варіантів досліджуваного процесу вибирають по будь-якою ознакою найкращий, оптимальний, варіант.
Прикладом такого завдання є завдання оптимального розподілу сировини між різними виробництвами при максимальній вартості продукції.
Нехай з двох видів сировини виготовляється продукція двох видів.
Позначимо: x 1. x 2 - число одиниць продукції першого і другого виду, відповідно; c 1. c 2 - ціна одиниці продукції першого і другого виду, відповідно. Тоді загальна вартість всієї продукції буде.
Побудуємо в системі прямокутних координат x 1 Ox 2 область допустимих рішень задачі (рис.11). Для цього, замінюючи кожне з нерівностей (5.5) рівністю, будуємо відповідну йому граничну пряму:
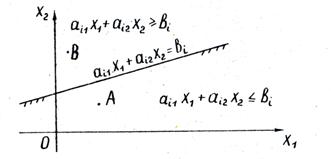
Ця пряма ділить всю площину на дві півплощини. Для координат x 1. x 2 будь-якої точки А одній півплощині виконується нерівність:
а для координат будь-якої точки В іншій півплощині - протилежне нерівність:
Координати будь-якої точки граничної прямої задовольняють рівняння:
Для визначення того, по який бік від граничної прямої розташовується напівплощина, відповідна заданому нерівності, досить «випробувати» одну якусь точку (найпростіше точку О (0; 0)). Якщо при підстановці її координат в ліву частину нерівності воно задовольняється, то напівплощина звернена в сторону до випробуваної точці, якщо ж нерівність не задовольняється, то відповідна полуплоскость звернена в протилежну сторону. Напрямок полуплоскости показується на кресленні штрихуванням. нерівності:
відповідають півплощині, розташовані праворуч від осі ординат і над віссю абсцис.
На малюнку будуємо граничні прямі і півплощини, які відповідають усім неравенствам.
Загальна, частина (перетин) всіх цих напівплощин буде являти собою область допустимих варіантів розв'язання задачі.
При побудові області допустимих рішень в залежності від конкретного виду системи обмежень (нерівностей) на змінні може зустрітися один з наступних чотирьох випадків:
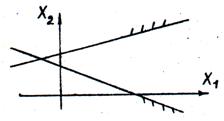
Мал. 12. Область допустимих рішень порожня, що відповідає несумісності системи нерівностей; рішення немає
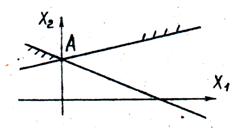
Мал. 13. Область допустимих рішень зображується однією точкою А. що відповідає єдиного рішення системи
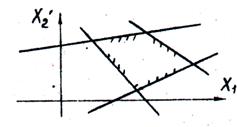
Мал. 14. Область допустимих рішень обмежена, зображується у вигляді опуклого багатокутника. Допустимих рішень безліч

Мал. 15. Область допустимих рішень необмежена, у вигляді випуклої багатокутної області. Допустимих рішень безліч
Графічне зображення цільової функції
при фіксованому значенні R визначає пряму. а при зміні R - сімейство паралельних прямих з параметром R. Для всіх точок, що лежать на одній з прямих, функція R прини-томить одне певне значення, тому зазначені прямі називаючи-ються лініями рівня для функції R.
перпендикулярний до ліній рівня, показує напрям зростання R.
Завдання відшукання оптимального рішення системи нерівностей (5.5), для якого цільова функція R (5.7) досягає максимуму, гео-метрично зводиться до визначенні-ня в області допустимих реше-ний точки, через яку пройде лінія рівня, відповідаю-щая найбільшому значенні пара- метра R
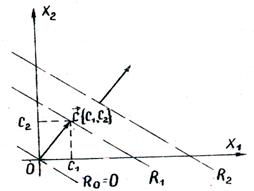
Якщо область допустимих рішень є опуклий багатокутник, то екстремум функції R досягається, по крайней мере, в одній з вер-шин цього багатокутника.
Якщо екстремальне значення R досягається в двох вершинах, то таке ж екстремальне значення досягається в будь-якій точці на відрізку, що з'єднує ці дві вершини. У цьому випадку говорять, що завдання має альтернативний оптимум.
У разі необмеженої області екстремум функції R або не існує, або досягається в одній з вершин області, або має альтернативний оптимум.
Нехай потрібно знайти значення x 1 і x 2. задовольняють системі нерівностей:
і умов невід'ємності.
для яких функція:
Замінимо кожне з нерівностей рівністю і побудуємо граничні прямі:
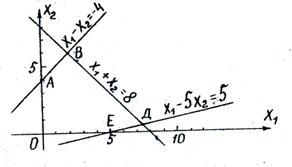
Визначимо півплощини, відповідні даними неравенствам, шляхом «випробування» точки (0; 0). З урахуванням невід'ємності x 1 і x 2 отримаємо область допустимих варіантів розв'язання задачі у вигляді опуклого багатокутника ОАВДЕ.
В області допустимих рішень знаходимо оптимальне рішення, будуючи вектор градієнта
показує напрямок зростання R.
Оптимальне рішення відповідає точці В. координати якої можна визначити або графічно, або шляхом вирішення системи двох рівнянь, відповідних граничним прямим АВ і ВД:
Завдання. Знайти положення точки екстремуму і екстремальне значення цільової функції
при заданих обмеженнях.