Метод відсікань Гоморі

Головна | Про нас | Зворотній зв'язок
У завданнях цілочисельного програмування на відміну від завдань лінійного програмування вводиться додаткове обмеження на змінні величини: вони можуть приймати лише цілі значення.
У деяких завданнях, наприклад, транспортного типу, ця умова виконується автоматично, якщо вихідні дані (кількості відправлених і отриманих вантажів) виражені цілими числами. Але в загальному завданню лінійного програмування звичайні методи вирішення целочисленности не гарантують, незалежно від того, цілими чи дробовими є вихідні величини.
У математичної записи спільне завдання цілочисельного програмування виглядає наступним чином:
Економічні задачі лінійного програмування найчастіше вимагає цілочисельного рішення. Це відноситься до завдань, в яких змінні величини позначають кількість одиниць неподільної продукції, обладнання, працівників (задачі найкращого розподілу виробничих завдань між підприємствами, завдання оптимізації виробничої програми окремих підприємств, завдання оптимального завантаження устаткування і ін.). Часто такі завдання вирішуються звичайним симплекс-методом з наступним округленням отриманих значень змінних величин до цілих чисел. Але в цьому випадку можна отримати лише деяке наближення до дійсно оптимальному целочисленному плану.
В іншій групі завдань лінійного програмування підлягають визначенню величинами є виробничі потужності, найбільш ефективно забезпечують задану потреба. Оскільки «носіями» виробничої потужності виступають окремі підприємства, неподільні одиниці обладнання і т. Д. Ці завдання також зводяться до цілочисельним завданням лінійного програмування.
Цілочисельними є також завдання раціонального розкрою мірного матеріалу (завдання на мінімум відходів), так як змінні позначають у них, як правило, кількість вихідних заготовок, розкроюють тим чи іншим способом.
У всіх згаданих задачах рішення може бути знайдено звичайними методами лінійного програмування з подальшим коректуванням і одержанням целочисленного плану, більш-менш близького до оптимального. Але є завдання, нецелочисленное вирішення яких не має сенсу. До них відносяться завдання вибору, в яких чисельні значення змінних служать лише для визначення альтернативи ( «або - або», «так - ні»).
До цілочисельним моделям вибору відносять деякі завдання оперативно-календарного планування, наприклад, завдання про оптимальну послідовності запуску різних виробів (деталей) у виробництво. Припустимо необхідно визначити порядок запуску n деталей, кожна з яких послідовно обробляється на декількох верстатах. Змінні хij дорівнюють одиниці, якщо деталь j повинна запускатися за деталлю i. і нулю - у всіх інших випадках. Для кожного фіксованого j. так само як і для кожного i. тільки одна з n змінних може дорівнювати одиниці, тому в число обмежень завдання входять наступні:
Мінімізується загальний час обробки всіх деталей на верстатах даної групи. Нецілочисельне рішення такого завдання позбавлене сенсу.
Існує кілька методів вирішення завдань цілочисельного програмування. Найбільш відомий метод Гоморі. грунтується на використанні симплексного методу.
Розглянемо математичні поняття: конгруентності чисел, цілої і дробової частини числа. Число а конгруентно числу b в тому і тільки тому випадку, коли різниця а - b є цілим числом. Конгруентність позначають трьома горизонтальними рисками (≡); таким чином, а ≡ b. якщо а - b є ціле число.
Всі цілі числа конгруентний один одному і конгруентний нулю. Нецілочисельне елементи можна представити у вигляді суми цілої і дробової частини числа а = [a] + a>. Квадратні дужки означають взяття цілої частини числа, укладеного в них, фігурні - взяття дробової частини числа.
Властивості конгруентності чисел:
При вирішенні завдань цілочисельного програмування методом Гоморі перший етап збігається зі звичайним розрахунком по сімплексному алгоритму. Отримане рішення в загальному вигляді буде відповідати всім умовам завдання, крім вимоги целочисленности (не виключено, звичайно, отримання цілочисельного рішення вже на першому етапі). Якщо серед значень змінних в оптимальному плані (точка А на рис.13) є дробові, то складається додаткове обмеження, як би «відтинає» дробову частину рішення (лінія 1 на рис.13), але залишає в силі всі обмеження задачі, яким повинен задовольняти оптимальний план. Додаткове обмеження приєднується до вихідних обмеженням завдання і до розширеної системи знову застосовується симплексна процедура. Якщо оптимальне рішення знову виявиться нецілочисельне (точка В на рис.13), то додається ще одне додаткове обмеження (лінія 2 на рис.13) і процес обчислень повторюється. Алгоритм дозволяє за кінцеве число кроків прийти до оптимального цілочисельного рішення (якщо воно існує) (точка С на рис.13).
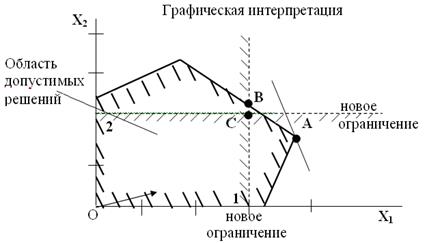
Мал. 13. Метод відсікань Гомори
Приклад рішення задачі цілочислового програмування. На придбання обладнання для нового виробничого ділянки виділено 20 грош Обладнання повинно бути розміщено на площі, що не перевищує 38 м 2. Підприємство може замовити обладнання двох видів: більш потужні машини типу А вартістю 5 ден.ед, що вимагають виробничу площу 8 м 2 (з урахуванням проходів) і забезпечують продуктивність 7 тис, одиниць продукції за зміну; менш потужні машини типу Б вартістю 2 ден.ед, що займають площу 4 м 2 і дають за зміну 3 тис, одиниць продукції.
Потрібно розрахувати оптимальний варіант придбання обладнання, що забезпечує при даних обмеженнях максимум загальної продуктивності ділянки.
Позначимо через х1 кількість придбаних машин А і через х2 - кількість придбаних машин Б, отримуємо математичні умови задачі:
максимізувати 7х1 + 3х2 → max
за умов: 5х1 + 2х2 ≤ 20
За допомогою додаткових змінних х3 і х4 вихідні нерівності перетворюються в рівняння (приводяться до канонічного виду):
Якщо основні змінні х1 і х2 - цілі числа, то з рівнянь безпосередньо випливає, що і змінні х3 і х4 можуть приймати тільки цілочисельні значення.
Завдання вирішується спочатку без урахування вимоги целочисленности.
Симплексна таблиця має такий вигляд:
В оптимальному плані Х1 = 1, Х2 = 7,5; максимум цільової функції становить 29,5. Таким чином, необхідно купити один верстат типу А і 7 верстатів типу В (на 8 верстатів не вистачить ні грошей, ні місця), тоді обсяг випуску продукції складе f (x) = 7 × 1 + 3 × 7 = 28 тис. Одиниць продукції .
Знайдемо целочисленное рішення методом Гоморі. Для змінної Х2. отримала нецелочисленное значення в плані, складаємо наступне рівняння, безпосередньо випливає з наведеної симплексной таблиці:
Це рівняння, очевидно, має бути справедливо і для допустимого цілочисельного рішення задачі.
Оскільки Х2 - ціле число, то цілим є і вираз в правій частині рівняння; отже, величина правій частині даного рівняння конгруентна нулю:
З огляду на наведені вище властивості конгруентності, а також і те, що Х3 і Х4 - цілі числа, цей вислів можна перетворити в такий спосіб:
Оскільки X4 - невід'ємне ціле число, маємо:
0,25X4 = 0,5, або 1,5, або 2,5. ;
Отримане нерівність перетворюється в рівняння і додається до вихідної системи обмежень, яка містить тепер такі три рівняння:
Повторивши процес вирішення симплексним методом стосовно розширеної системі обмежень, отримаємо новий оптимальний план, в якому значення змінних, що входять в базис, дорівнюють: Х1 = 2; Х2 = 5; Х4 = 2 (залишок вільної площі).
Таким чином, отримано оптимальне цілочисельне рішення задачі: при даних обмеженнях максимум продуктивності (29 тис. Одиниць продукції) забезпечується придбанням 2 машин типу А і 5 машин типу Б.
МЕТОД ГІЛОК І МЕЖ
Цей метод можна застосувати для вирішення як повністю, так і частково цілочисельних задач дискретного програмування.
Припустимо, що для кожної цілочисельний змінної можна задати верхню і нижню межі, в межах яких, безумовно, містяться її оптимальні значення
Зазвичай Hj = 0, але ця умова не обов'язково. Завдання вирішується симплекс-методом. Якщо Xk приймає дробові значення, то вважаємо, що оптимальне рішення задачі, буде задовольняти лінійному обмеження Xk ≤ Dk. або лінійному обмеження Xk ≤ Dk + 1. де Dk = [Xk] - найближче ціле число в меншу сторону від значення Xk; Dk + 1 - найближче ціле в більшу сторону від Xk. При цьому Hj ≤ Dk ≤ Vj - 1. Тоді необхідно вирішити пару завдань лінійного програмування симплекс-методом:
Отримуємо ітераційний процес, що представляється у вигляді дерева, вершина якого відповідає рішенню вихідної задачі, а дві з'єднані з нею гілки є рішеннями пари задач лінійного програмування А і В. Отримані значення цільових функцій при цьому можуть бути менше або дорівнюють значенню цільової функції вихідної задачі f ( X) A ≤ f (X) -0; f (X) B ≤ f (X) -0. Кожна з двох нових отриманих вершин гілок може мати свої подальші розгалуження.
1) Ітераційний процес розгалуження триває до тих пір, поки серед отриманих планів не буде отримано цілочисельне рішення, причому значення цільової функції має бути більшим чи рівним значенням функцій цілей інших розгалужених вершин.
2) Якщо на черговому кроці ітерації обидва завдання мають нецілочисельне рішення, то для подальшого розгалуження вибирається вершина, відповідна задача з великим значенням функції мети. Для однієї з змінних, які отримали дробові значення, складаються нові обмеження для наступних завдань лінійного програмування.
3) Якщо на черговому кроці ітерації одне із завдань має целочисленное рішення, а серед значень змінних на другий завданню є дробові, то з них вибирається завдання, що має найбільше значення функції мети. Якщо це завдання, що отримала целочисленное рішення, то процес закінчується, якщо ж ця задача з дробовими значеннями змінних, то для неї виробляється подальший процес розгалуження.
4) Якщо на черговому кроці ітерації одне із завдань не має рішення, а друга завдання серед значень змінних в одержуваному вирішенні має дробові величини. Тоді для першого завдання процес розгалуження припиняється, а для подальшого перетворення другого завдання вибирається одна з нецілочисельне змінних, для якої складаються додаткові обмеження для нової пари задач лінійного програмування.
5) Якщо на черговому кроці ітерації одне із завдань не має рішення, а для іншої отримано цілочисельне рішення, і немає інших варіантів з великим цілочисельним значенням функції мети і для яких можна продовжувати розгалуження, то процес закінчується, а знайдене рішення є оптимальним цілочисельним рішенням вихідної завдання.
Якщо обрана задача призводить до обриву (тупику) або значення функції меншому, ніж в завданні В.1f (X) A.4 Схожі статті