Мережа Хопфілда - студопедія
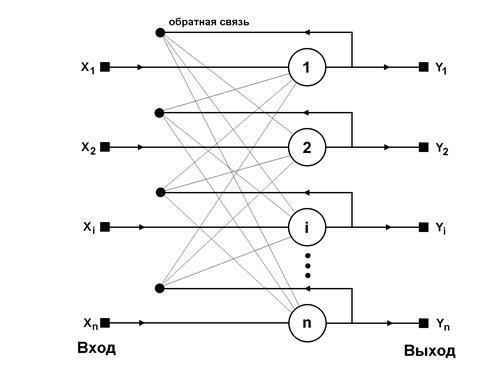
Мал. 6.1 Узагальнена структура мережі Хопфілда
Це означає, що вихідний сигнал нейрона визначається функцією:
де позначає число нейронів.
Будемо вважати, що порогові елементи є компонентами вектора. Без урахування одиничних затримок мережі, що представляють собою спосіб синхронізації процесу передачі сигналів, основні залежності, що визначають мережу Хопфілда, можна представити у вигляді:
з початковою умовою. В процесі функціонування мережі Хопфілда можна виділити два режими: навчання і класифікації. У режимі навчання на основі відомих навчальних вибірок підбираються вагові коефіцієнти. У режимі класифікації при зафіксованих значеннях ваг і введення конкретного початкового стану нейронів виникає перехідний процес, що протікає відповідно до вираження (6.5) і завершується в одному з локальних мінімумів, для якого.
При введенні тільки однієї навчальної вибірки процес змін триває до тих пір, поки залежність (6.5) не почне дотримуватися для всіх нейронів. Ця умова автоматично виконується в разі вибору значень ваг, що відповідають відношенню
оскільки тільки тоді (внаслідок біполярних значень елементів вектора завжди виконується співвідношення). Слід зазначити, що залежність (6.6) являє собою правило навчання Хебба. При введенні великої кількості навчальних вибірок для ваги підбираються згідно узагальненому правилом Хебба, відповідно до якого
Завдяки такому режиму навчання ваги набувають значень, які визначаються усередненням безлічі навчальних вибірок.
У разі безлічі навчальних вибірок стає актуальним фактор стабільності асоціативної пам'яті. Для стабільного функціонування мережі необхідно, щоб реакція -го нейрона на -у навчальну вибірку збігалася з її -й складової. Це означає, що з урахуванням виразу (6.7) отримаємо
Якщо зважену суму вхідних сигналів -го нейрона позначити, то можна виділити в ній очікуване значення і залишок, званий Діафон [4]:
Внаслідок застосування знаковою функції активації, виконання умови (6.8) можливо при малих значеннях Діафон, нездатних змінити знак. Це означає, що, незважаючи на певне розбіжність бітів, перехідний процес завершується в потрібній точці тяжіння. При наданні тестової вибірки, що відрізняється деякою кількістю бітів, нейронна мережа може відкоригувати ці біти і завершити процес класифікації в потрібній точці тяжіння.
Проте, правило Хебба володіє невисокою продуктивністю. Максимальна місткість асоціативної пам'яті (число запам'ятали зразків) при навчанні за правилом Хебба з допустимою похибкою 1%, становить приблизно 14% від числа нейронів мережі [4]. Крім того, при наявності шуму, застосування правила Хебба призводить до різних неточностей у вигляді локальних мінімумів, далеких від вихідного рішення. Тому в якості альтернативи використовують методи навчання, засновані на псевдоінверсії.
де - матриця ваг мережі розмірністю, а - прямокутна матриця розмірністю, складена з послідовних навчальних векторів, тобто. Рішення такої лінійної системи рівнянь має вигляд:
де знак + означає псевдоінверсії. Якщо навчальні вектори лінійно незалежні, останній вираз можна представити у формі:
Псевдоінверсії матриці розмірністю в цьому виразі замінена звичайної інверсією квадратної матриці розмірністю. Додаткова перевага вираження (6.12) - можливість записати його в итерационной формі, яка не потребує розрахунку оберненої матриці. В цьому випадку вираз (6.12) набирає вигляду функціональної залежності від послідовності навчальних векторів для:
при початкових умовах. Така форма передбачає одноразове пред'явлення всіх навчальних вибірок, в результаті чого матриця ваг приймає значення. Залежності (6.12) і (6.13) називаються методом проекцій. Застосування методу псевдоінверсії збільшує максимальну ємність мережі Хопфілда, яка стає рівною.
Модифікований варіант методу проекцій - метод проекцій - це градиентная форма алгоритму мінімізації цільової функції. Відповідно до цього способом ваги підбираються рекуррентно за допомогою циклічної процедури, повторюваною для всіх навчальних вибірок:
Коефіцієнт - це коефіцієнт навчання, обираний зазвичай з інтервалу [0.7 - 0.9]. Процес навчання завершується, коли зміна вектора ваг стає менше апріорно прийнятого значення.
По завершенні підбору ваг мережі їх значення «заморожуються», і мережу можна використовувати в режимі розпізнавання. У цій фазі на вхід мережі подається тестовий вектор і розраховується її відгук у вигляді:
(В початковий момент), причому ітераційний процес повторюється для послідовних значень аж до стабілізації відгуку.
У процесі розпізнавання образу за зашумленими сигналам, що створює початковий стан нейронів, виникають проблеми з визначенням кінцевого стану, відповідного одному з запам'ятали образів. Можливі помилкові рішення. Однією з причин знаходження помилкових рішень є можливість перемішування різних компонентів, що запам'ятали образів і формування стабільного стану, яка сприймається як локальний мінімум.