Лекція 2 незсунені, ефективні і спроможні оцінки параметрів розподілу

Для того, щоб статистичні оцінки давали гарне наближення оцінюваних параметрів, вони повинні бути незсунені, ефективні і заможні.

Незміщеної називається статистична оцінка

параметра, математичне очікування якої дорівнює оцінюваному параметру при будь-якому обсязі вибірки.

Зміщеною називається статистична оцінка

параметра, математичне очікування якої не дорівнює оцінюваному параметру.

Ефективною називається статистична оцінка

параметра, яка при заданому обсязі вибіркимає найменшу дисперсію.

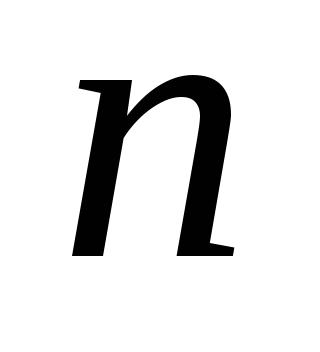
Заможної називається статистична оцінка

параметра, яка припрагне за ймовірністю до оцінюваного параметру.

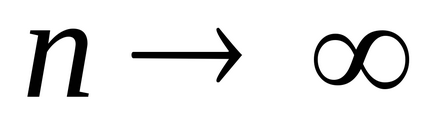
Для вибірок різного обсягу виходять різні значення середнього арифметичного і статистичної дисперсії. Тому середнє арифметичне і статистична дисперсія є випадковими величинами, для яких існують математичне очікування і дисперсія.

Обчислимо математичне сподівання середнього арифметичного і дисперсії. позначимо через

математичне сподівання випадкової величини

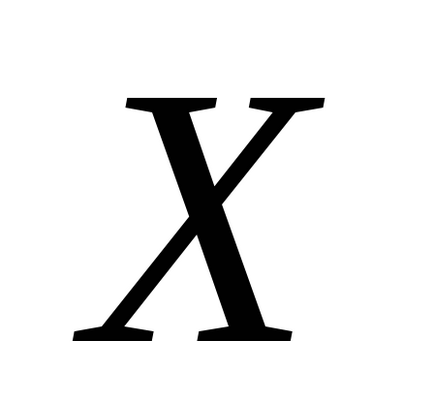
Тут в якості випадкових величин розглядаються:

- С.В. значення якої дорівнюють першим значенням, отриманим для різних вибірок обсягуз генеральної сукупності,-С.В. значення якої дорівнюють другим значенням, отриманим для різних вибірок обсягуз генеральної сукупності, ...,- С.В. значення якої дорівнюють-м значенням, отриманим для різних вибірок обсягуз генеральної сукупності. Всі ці випадкові величини розподілені по одному і тому ж закону і мають одне і те ж математичне очікування.

.

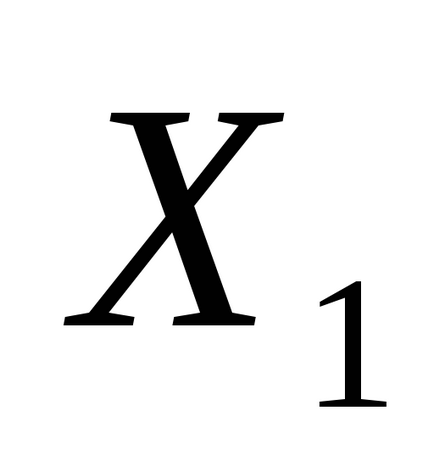
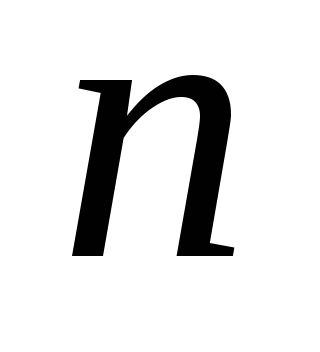
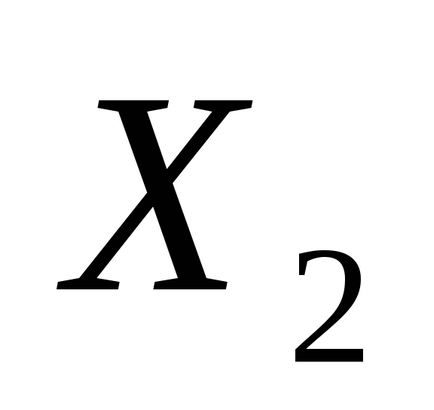
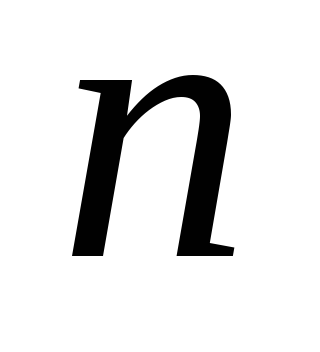
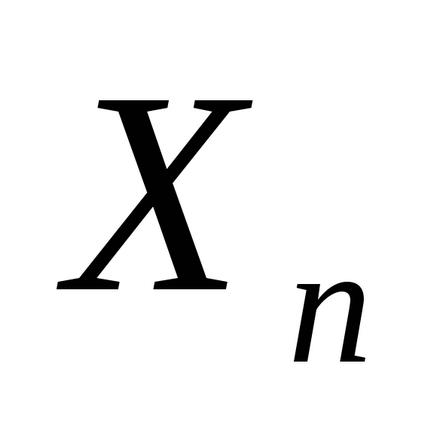
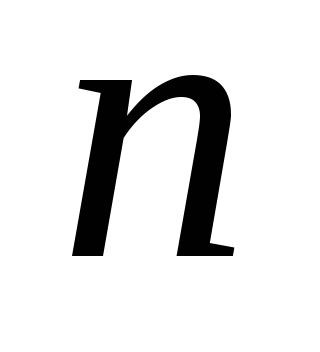
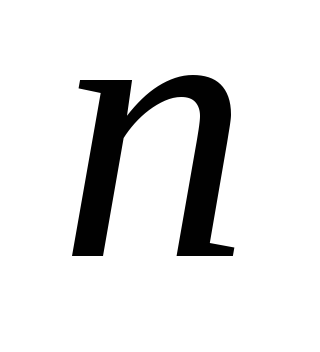
З формули (1) випливає, що середнє арифметичне є несмещенной оцінкою математичного очікування, так як математичне очікування середнього арифметичного одно математичного сподівання випадкової величини. Ця оцінка є також заможної. Ефективність даної оцінки залежить від виду розподілу випадкової величини

. Якщо, наприклад,розподілена нормально, оцінка математичного очікування за допомогою середнього арифметичного буде ефективною.

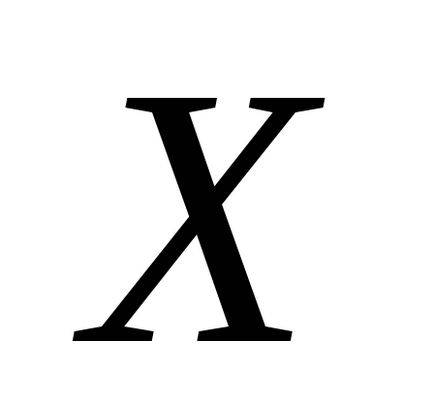
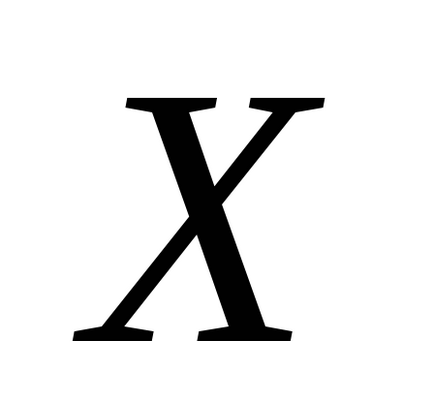
Знайдемо тепер статистичну оцінку дисперсії.

Вираз для статистичної дисперсії можна перетворити в такий спосіб

Знайдемо тепер математичне очікування статистичної дисперсії

З формули (6) видно, що математичне очікування статистичної дисперсії відрізняється множником від дисперсії, тобто є зміщеною оцінкою дисперсії генеральної сукупності. Це пов'язано з тим, що замість істинного значення

, яке невідомо, в оцінці дисперсії використовується статистичне середнє.

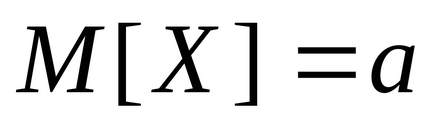
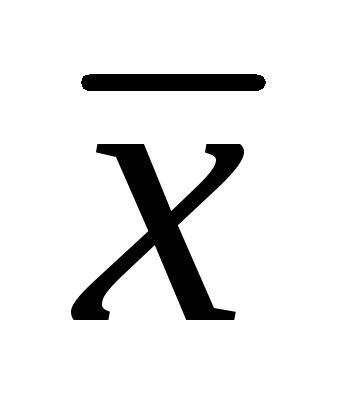
Тому введемо виправлену статистичну дисперсію

Тоді математичне очікування виправленої статистичної дисперсії одно

тобто виправлена ​​статистична дисперсія є несмещенной оцінкою дисперсії генеральної сукупності. Отримана оцінка є також заможної.