Котушка індуктивності в колі змінного струму
Мета роботи . вивчення поведінки соленоїда в ланцюгах постійного і змінного струму, експериментальне визначення індуктивності котушки з всувають в неї феромагнітним сердечником.
Явище електромагнітної індукції.
Поняття індуктивності контуру
У всякому замкнутому провідному контурі при зміні потоку магнітної індукції через поверхню, обмежену контуром, виникає електричний струм, який називається індукційним струмом. Це явище було відкрито в 1831 році Фарадеєм і названо явищем електромагнітної індукції. Якщо проводить контур помістити в змінне магнітне поле (рис. 1), то між точками 1 і 2 провідники виникає електрорушійна сила індукції, чисельно рівна швидкості зміни потоку магнітної індукції через поверхню S (закон Фарадея):
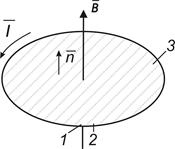
При цьому потік магнітної індукції може змінюватися як в результаті руху контуру в постійному магнітному полі, так і за рахунок зміни індукції магнітного поля в часі, коли контур нерухомий. У першому випадку індукційний струм викликається магнітною складовою сили Лоренца. Але яка ж сила збуджує індукційний струм в нерухомому контурі? Відповідь на це питання була дана Максвеллом. Згідно з його висновком, всяке змінне магнітне поле збуджує в навколишньому просторі змінне електричне поле. Згідно Фарадею, електромагнітна індукція полягає в порушенні електричного струму при наявності замкнутого провідника. Максвелл ж визначив сутність електромагнітної індукції, перш за все в порушенні електричного поля. а не струму. При цьому електричне поле виробляє різні дії, наприклад, воно може поляризувати діелектрик, викликати пробій конденсатора, може створити ток як в замкнутому, так і в незамкнутому провіднику. Формулювання закону індукції Максвелла є більш загальною, ніж формулювання Фарадея. Математично закон індукції в розумінні Максвелла виражається формулою (1), де S - довільний математичний замкнутий контур, який може бути проведений в провіднику, в діелектрику і т.д.
Знак мінус в співвідношенні (1) висловлює правило Ленца. індукційний струм спрямований таким чином, що створюваний ним потік через поверхню протидіє зміні зовнішнього магнітного потоку, яке викликає появу індукційного струму в контурі. Якщо зовнішнього магнітного поля немає, а по контуру тече змінний струм I. то він викликає поява змінного власного магнітного поля. Зміна магнітного потоку індукує ЕРС не тільки в інших провідниках, але і в самому контурі, що створює це магнітне поле. Це явище називається самоіндукцією. Самоіндукція особливо сильно проявляється при замиканні або розмиканні ланцюгів. Вона перешкоджає стрибкоподібної зміни струму. Потік самоіндукції пропорційний току:
а закон Фарадея (1) переписується у вигляді:
Коефіцієнт пропорційності L в формулах (2) і (3) є електричної характеристикою даного контуру і називається індуктивністю контуру.
Значення величини L залежить від геометричної форми контуру, його розмірів і відносної магнітної проникності середовища. в якій знаходиться контур. Наприклад, індуктивність соленоїда довжиною l. із загальним числом витків N і площею одного витка S визначається формулою:
Зі співвідношення (3) видно, що величина індуктивності контуру чисельно дорівнює ЕРС самоіндукції в контурі при зміні в ньому сили струму на одиницю за одну секунду (при). Це визначає ФИЗИЧЕСКИЙ СЕНС поняття індуктивності контуру E. Вона є мірою "інертності" контуру по відношенню до зміни струму в ньому. У цьому сенсі індуктивність L контуру в електродинаміки грає таку ж роль, як маса або момент інерції в механіці. За одиницю вимірювання індуктивності L в системі СІ приймається індуктивність такого контуру, в якому при силі струму в 1А виникає магнітний потік Ф, що дорівнює 1Вб (вебер). Цю одиницю називають Генрі (Гн). Якщо електричне коло містить кілька индуктивностей, послідовно з'єднаних один з одним, то еквівалентна індуктивність визначається формулою:
У разі паралельного з'єднання декількох индуктивностей в ланцюзі залежність набуває вигляду:
У даній лабораторній роботі для визначення індуктивності котушки використовується змінний електричний струм, значення якого змінюється в часі за гармонійним законом. Гармонійні коливання можна представити у вигляді проекції точки рівномірно рухається по колу. Подання гармонійних коливань за допомогою обертових векторів називається векторною діаграмою. Якщо вектор А обертається з кутовою швидкістю навколо центру проти годинникової стрілки, то проекція кінця цього вектора на вісь ОХ здійснює гармонійне коливання уздовж осі X. Рівняння цього коливання:
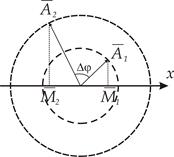
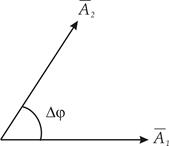
Обертається вектор називається вектором амплітуди. Кут повороту вектора в даний момент часу t чисельно дорівнює фазі коливання за цей проміжок часу. Якщо є два коливання, які відбуваються з однаковою круговою частотою і з різницею фаз. то їх можна зобразити за допомогою двох векторів амплітуди і розташованих під кутом один до одного (рис. 2). В цьому випадку точки і коливаються з різницею фаз. Прийнято зображати положення векторів амплітуди в початковий момент часу вважаючи, що їх обертання відбувається проти годинникової стрілки (рис. 3).
Між напругою і струмом в ланцюзі, що містить тільки .індуктівность, виникає різниця фаз (зрушення фаз) рівна. тобто напруга випереджає струм на (або Т / 4).
Дуже наочно отриманий результат можна зобразити на векторній діаграмі (рис. 5).
Горизонтальну вісь приймемо за вісь струмів. Відкладемо уздовж цього напрямку вектор струму, чисельно рівний амплітудному значенням струму. Так як напруга випереджає струм за фазою на. то вектор повернуть щодо осі струмів на проти годинникової стрілки. З рівності (5) випливає, що амплітуда напруги. Розділивши праву і ліву частини цього виразу на. отримаємо закон Ома для ланцюга з індуктивністю:
де і - ефективні (діючі) значення напруги і струму.
На практиці звичайні вольтметри і амперметри в колі змінного струму показує не амплітудні (максимальні) значення струму і напруги, а саме ефективні значення, які в раз їх менше. Таким чином, з закону Ома ми бачимо, що величина грає роль опору змінному струмі і називається індуктивним опором.
Послідовне з'єднання резистивного, індуктивного
і ємнісного елементів в колі змінного струму
Зазвичай реальна електричний ланцюг являє собою досить складну комбінацію індуктивного, ємнісного і омічного опору. Розглянемо простий випадок послідовного з'єднання індуктивності, ємності і резистора (рис. 6).
Згідно з другим законом Кірхгофа, рівняння для миттєвих значень напруг в такому колі має вигляд:
Так як в даному випадку загальним для всіх ділянок ланцюга є струм, то доцільно вибрати його початкову фазу, рівну 0. Відомо, що напруга на резистивном елементі збігається по фазі з струмом ланцюга, на індуктивному елементі напруга випереджає струм на кут. а напруга на ємності відстає від струму на кут.
Тоді, висловивши напруга через струм і відповідні опору ділянок ланцюга, отримаємо:
Амплітудне значення напруги, прикладеної до ланцюга Um одно векторної сумі напруг на всіх елементах ланцюга, тобто
Додавання цих трьох векторів легко провести на векторній діаграмі. Трикутник ОАВ на векторній діаграмі напруг (рис. 7) називають трикутником напружень.
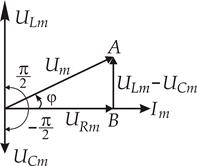
У загальному вигляді вираз для миттєвого значення напруги в ланцюзі в залежності від значення L або C можна записати так:. З урахуванням цього запису рівняння (7) набуває вигляду: